洛谷 P3745 [六省联考2017]期末考试 题解【贪心】【三分】
点击量:171
今天学了一下三分……然而这个题可以枚举orz
题目描述
有\(n\)位同学,每位同学都参加了全部的\(m\)门课程的期末考试,都在焦急的等待成绩的公布。
第\(i\)位同学希望在第\(t_i\)天或之前得知所有课程的成绩。如果在第\(t_i\)天,有至少一门课程的成绩没有公布,他就会等待最后公布成绩的课程公布成绩,每等待一天就会产生\(C\)不愉快度。
对于第\(i\)门课程,按照原本的计划,会在第\(b_i\)天公布成绩。
有如下两种操作可以调整公布成绩的时间:
- 将负责课程\(X\)的部分老师调整到课程\(Y\),调整之后公布课程\(X\)成绩的时间推迟一天,公布课程\(Y\)成绩的时间提前一天;每次操作产生\(A\)不愉快度。
- 增加一部分老师负责学科\(Z\),这将导致学科\(Z\)的出成绩时间提前一天;每次操作产生\(B\)不愉快度。
上面两种操作中的参数\(X,Y,Z\)均可任意指定,每种操作均可以执行多次,每次执行时都可以重新指定参数。
现在希望你通过合理的操作,使得最后总的不愉快度之和最小,输出最小的不愉快度之和即可。
输入输出格式
输入格式:
第一行三个非负整数\(A,B,C\),描述三种不愉快度,详见【题目描述】;
第二行两个正整数\(n,m\),分别表示学生的数量和课程的数量;
第三行\(n\)个正整数\(t_i\),表示每个学生希望的公布成绩的时间;
第四行\(m\)个正整数\(b_i\),表示按照原本的计划,每门课程公布成绩的时间。
输出格式:
输出一行一个整数,表示最小的不愉快度之和。
输入输出样例
输入样例#1:
100 100 2 4 5 5 1 2 3 1 1 2 3 3输出样例#1:
6输入输出样例 1 说明:
由于调整操作产生的不愉快度太大,所以在本例中最好的方案是不进行调整;全部的\(5\)门课程中,最慢的在第\(3\)天出成绩;
同学\(1\)希望在第\(5\)天或之前出成绩,所以不会产生不愉快度;
同学\(2\)希望在第\(1\)天或之前出成绩,产生的不愉快度为\((3-1)\times 2=4\);
同学\(3\)希望在第\(2\)天或之前出成绩,产生的不愉快度为\((3-2)\times 2=2\);
同学\(4\)希望在第\(3\)天或之前出成绩,所以不会产生不愉快度;
不愉快度之和为\(4+2=6\)。输入样例#2:
3 5 4 5 6 1 1 4 7 8 2 3 3 1 8 2输出样例#2:
33数据范围与约定
测试点 \(n, m, t_i, b_i\) \(A,B,C\) \(1,2\) \(1\leq n,m,t_i,b_i\leq 2000\) \(A=10^9,B=10^9,0\leq C\leq 10^2\) \(3,4\) \(0\leq A,C\leq 10^2,B=10^9\) \(5,6,7,8\) \(0\leq B\leq A\leq 10^2,0\leq C\leq 10^2\) \(9,10,11,12\) \(0\leq A,B,C\leq 10^2\) \(13,14\) \(1\leq n,m,t_i,b_i\leq 10^5\) \(0\leq A,B\leq 10^5,C=10^{16}\) \(15,16,17,18,19,20\) \(0\leq A,B,C\leq 10^5\)
题解:
首先分析一下本题的模型。可以想象成一个木桶效应,即“短板”的来源。

如图,即使最快改完卷子的课程用时为(0),它也需要等待最慢改完卷子的课程。因此在改卷的人力定下来之后,全部课程改卷结束的时间是唯一的。既然不愉快度是由人力决定的,人力的改变也决定了完成的时间。
因此我们尝试确定一个结束时间,这样再贪心地分配人力,就可以求出以这个时间结束的最小不愉快度。

虚线此时是要求改完卷子的时间,那么在虚线右边的时间就需要通过调度老师或者增加老师来弥补。首先判断是否有(A\le B),如果是,则虚线左边的空隙都可以拿来填补虚线右边的时间条,剩下的(若(A>B),则剩下的就还是原来那么多)需要拿(B\times)天数来弥补。再根据学生的需要,把虚线左边的橙色线条到虚线的距离和都统计出来,乘上(C),就是我们把结束时间定在虚线位置的不愉快度。
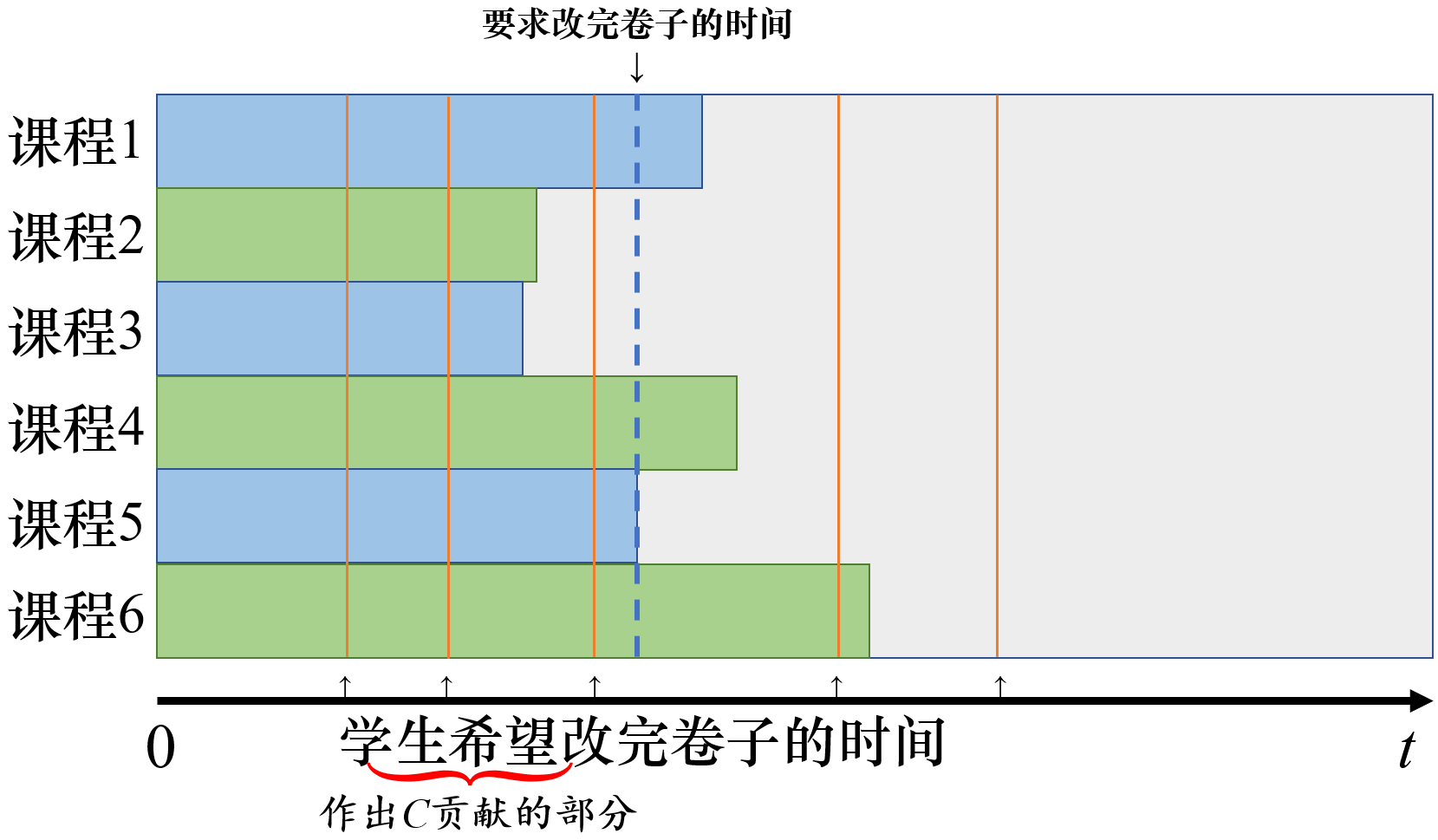
我们知道了这些,实际上就可以做这个题了,用两部分前缀和预处理一下,这个时间就可以从(maxb_i)向前枚举了。不过害怕前缀和出问题的话,可以想想三分,此时要证不愉快度是单峰的。三分好像不比前缀和好写到哪去。
假设我们现在有最优解(x=t),那么对于(x+a(a>0))来说,一定有(ans_{x+a}>ans_x)。
理由是随着改卷结束时间(虚线)的增加,出现在虚线以左的橙线会在个数和距离上都不断增加,尽管由(A,B)产生的不愉快度会减小,但只是杯水车薪,况且这个减小的幅度也会越来越小,最后趋近于(0)。可能会有人担心这个不愉快度减小得比(C)部分增加得快,如果存在某解比最优解更优,它一定与最优解相邻,既然相邻就会一定被三分过程更新到。
对于(x-a)同理,(A,B)产生贡献增加的幅度会越来越大,而(C)产生的贡献幅度会越来越小。因此三分的正确性可以保证。
那么我们就有了(O(m\log \max{b_i}))的优秀三分解法。再在三分内部使用前缀和,就可以做到(O(n+m+\log m))了好神经啊。
Code:
复杂度为(O(m\log \max{b_i})),会在计算函数内部多枚举一次
#include<cstdio>
#include<cstring>
#define ll long long
#define N 100005
ll read()
{
ll x=0;
char ch=getchar();
while(ch<'0'||ch>'9')
ch=getchar();
while(ch>='0'&&ch<='9')
{
x=x*10+ch-'0';
ch=getchar();
}
return x;
}
ll b[N],sum[N];//有多少人期望在第i天之前出成绩
ll sum1[N];//前面人的天数之和
ll x,y,z,n,m;
ll f[N];//记忆化在第i天出成绩的代价
ll calc(int u)//要求在第u天出成绩
{
if(f[u]!=-1)
return f[u];
f[u]=0;
ll r=0,t=0;//r表示有多少余力 t表示还需要多少
for(int i=1;i<=m;++i)
if(b[i]>u)
t+=b[i]-u;
else
r+=u-b[i];
//首先要填满 贪心看是调度便宜还是直接加便宜
if(x<y)
{
ll tmp=r<t?r:t;
f[u]+=tmp*x;
t-=tmp;
}
f[u]+=t*y;
f[u]+=(sum[u]*u-sum1[u])*z;
return f[u];
}
int main()
{
memset(f,-1,sizeof(f));
x=read();y=read();z=read();n=read();m=read();
int u,mn=N;
for(int i=1;i<=n;++i)
{
u=read();
++sum[u];
mn=mn<u?mn:u;
}
for(int i=1;i<N;++i)
{
sum1[i]=sum1[i-1]+sum[i]*i;
sum[i]+=sum[i-1];
}
for(int i=1;i<=m;++i)
b[i]=read();
int l=0,r=N-1,mid;
if(z==10000000000000000)
r=mn;
while(l<r)
{
mid=(l+r)>>1;
ll y_=calc(mid),y__=calc(mid+1);
if(y_==y__)
{
printf("%lld\n",y_);
return 0;
}
else if(y_>y__)
l=mid+1;
else
r=mid;
}
printf("%lld\n",calc(l));
return 0;
}计算函数可以改为
ll calc(int u)//要求在第u天出成绩
{
if(f[u]!=-1)
return f[u];
f[u]=0;
ll r=0,t=0;//r表示有多少余力 t表示还需要多少
r=Sum[u]*u-Sum1[u];
t=Sum1[N-1]-Sum1[u]-(Sum[N-1]-Sum[u])*u;
//首先要填满 贪心看是调度便宜还是直接加便宜
if(x<y)
{
ll tmp=r<t?r:t;
f[u]+=tmp*x;
t-=tmp;
}
f[u]+=t*y;
f[u]+=(sum[u]*u-sum1[u])*z;
return f[u];
}其中Sum[i]表示(i)前面有多少课程的改卷工作能完成;Sum1[i]表示课程完成的时间前缀和。


说点什么