洛谷 P4568 [JLOI2011]飞行路线 题解【图论】【分层图】

点击量：26

   分层图是用来解决有k次“删边”机会的最短路问题的一种做法。

目录

题目描述

Alice和Bob现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在n个城市设有业务，设这些城市分别标记为0到n-1，一共有m种航线，每种航线连接两个城市，并且航线有一定的价格。

Alice和Bob现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多k种航线上搭乘飞机。那么Alice和Bob这次出行最少花费多少？

输入输出格式

输入格式：

数据的第一行有三个整数，n,m,k，分别表示城市数，航线数和免费乘坐次数。
第二行有两个整数，s,t，分别表示他们出行的起点城市编号和终点城市编号。
接下来有m行，每行三个整数，a,b,c，表示存在一种航线，能从城市a到达城市b，或从城市b到达城市a，价格为c。

输出格式：

只有一行，包含一个整数，为最少花费。

 

输入输出样例

输入样例#1：

5 6 1

0 4

0 1 5

1 2 5

2 3 5

3 4 5

2 3 3

0 2 100

输出样例#1：

8

说明

对于30%的数据,2<=n<=50,1<=m<=300,k=0;

 

对于50%的数据,2<=n<=600,1<=m<=6000,0<=k<=1;

 

对于100%的数据,2<=n<=10000,1<=m<=50000,0<=k<=10,0<=s,t<n,0<=a,b<n,a≠b,0<=c<=1000.

   这个题也就是在图上删掉k条边使得此时的最短路解最优。

   这样我们就引入了分层图问题，也就是把图分成k层，就是可以有k次“免过路费”的权利。我们通过分层来控制删减并且只删减k条边的条件，对于一条边u->v，边权为w来说，它删掉当前边，就要跳到下一层去，说明用掉了一次机会。我们把初始状态设为第0层，那么第i层就是删掉i条边后的状态了。像下面的两层：

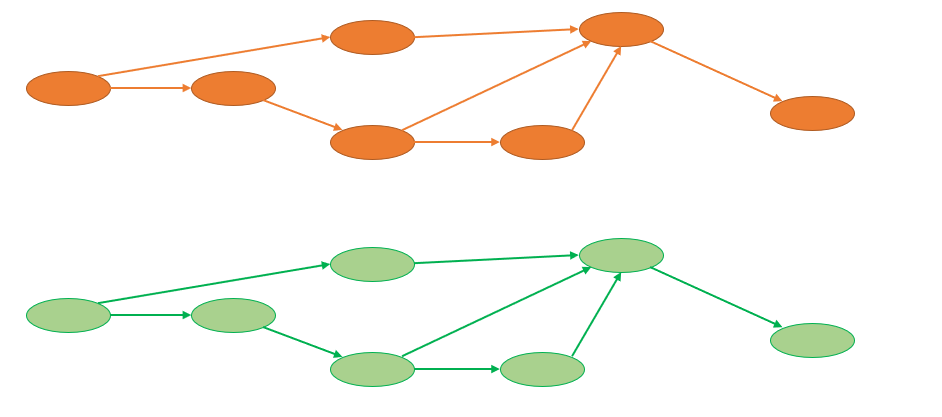
   我们把所有有向边都向下指一层，变成：

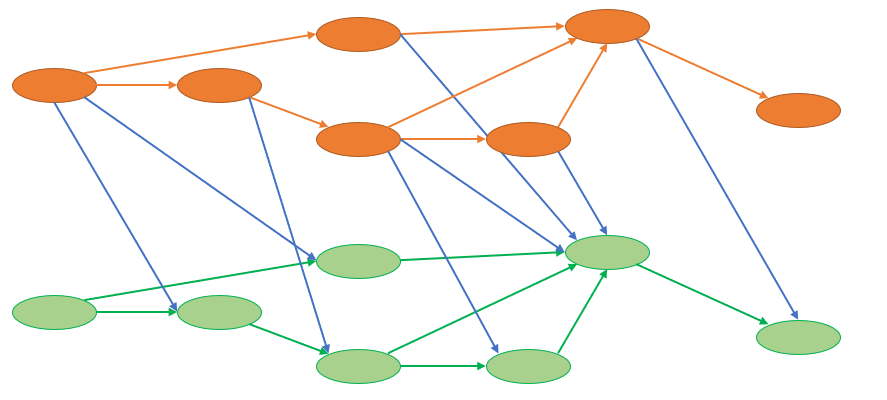
   当黄色和绿色的边都是有边权的边时，蓝色是没有边权的边，那么因为所有蓝色边是有向的（在无向图中也是），控制了只跳过k次这个条件，而点相当于是原来的k倍。这样我们直接在新图上跑最短路就可以了（原题卡SPFA）。

   我们有两种做法：第一种是建k×n个点的图，像图上一样连边，最后求到第k×n个点的最短路。第二种有点像动态规划/递推的思想，在dijkstra算法的结果数组中增加一维，上一维通过蓝色边连接到下一位是不需要边权的耗费的，于是这个转移方程是e=(u,v,w):f[v][k+1]=f[u][k](k!=h,h是原题中的k)，其他和最短路一样松弛就行了。

Code：

#include<cstdio>
#include<cstring>
#include<queue>
using std::priority_queue;
struct statu
{
    int n,r,v;
    statu(int n,int r,int v)
    {
        this->n=n;
        this->r=r;
        this->v=v;
    }
    statu(){}
    friend bool operator <(statu a,statu b)
    {
        return a.v>b.v;
    }
};
priority_queue<statu> q;
struct node
{
    int n,v;
    node *nxt;
    node(int n,int v)
    {
        this->n=n;
        this->v=v;
        nxt=NULL;
    }
    node()
    {
        nxt=NULL;
    }
};
node head[11000],*tail[11000];
int f[11000][15];
int s,t,h;
void dijk()
{
    f[s][0]=0;
    statu k(s,0,0);
    q.push(k);
    while(!q.empty())
    {
        k=q.top();
        q.pop();
        if(k.v>f[k.n][k.r])
            continue;
        node *p=&head[k.n];
        while(p->nxt!=NULL)//同层之间转移
        {
            p=p->nxt;
            if(k.v+p->v<f[p->n][k.r])
            {
                f[p->n][k.r]=k.v+p->v;
                q.push(statu(p->n,k.r,f[p->n][k.r]));
            }
        }
        if(k.r!=h)//跨层递推
        {
            p=&head[k.n];
            while(p->nxt!=NULL)
            {
                p=p->nxt;
                if(k.v<f[p->n][k.r+1])
                {
                    f[p->n][k.r+1]=k.v;
                    q.push(statu(p->n,k.r+1,f[p->n][k.r+1]));
                }
            }
        }
    }
}
int main()
{
    memset(f,0x3f,sizeof(f));
    int n,m;
    scanf("%d%d%d",&n,&m,&h);
    for(int i=0;i<n;i++)
        tail[i]=&head[i];

    scanf("%d%d",&s,&t);
    int u,v,w;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        tail[u]->nxt=new node(v,w);
        tail[u]=tail[u]->nxt;
        tail[v]->nxt=new node(u,w);
        tail[v]=tail[v]->nxt;
    }
    dijk();
    printf("%d\n",f[t][h]);
    return 0;
}