洛谷 P2598 [ZJOI2009]狼和羊的故事 题解【网络流】【最小割】【构造】

点击量：133

   一开始看这个题以为是bfs找最近两个栅栏并相连，不过好像时间复杂度还是有点高。最小割做法实在是优秀。

目录

题目描述

“狼爱上羊啊爱的疯狂，谁让他们真爱了一场；狼爱上羊啊并不荒唐，他们说有爱就有方向．．．．．．” Orez听到这首歌，心想：狼和羊如此和谐，为什么不尝试羊狼合养呢？说干就干！

 

Orez的羊狼圈可以看作一个n*m个矩阵格子，这个矩阵的边缘已经装上了篱笆。可是Orez很快发现狼再怎么也是狼，它们总是对羊垂涎三尺，那首歌只不过是一个动人的传说而已。所以Orez决定在羊狼圈中再加入一些篱笆，还是要将羊狼分开来养。

 

通过仔细观察，Orez发现狼和羊都有属于自己领地，若狼和羊们不能呆在自己的领地，那它们就会变得非常暴躁，不利于他们的成长。 Orez想要添加篱笆的尽可能的短。当然这个篱笆首先得保证不能改变狼羊的所属领地，再就是篱笆必须修筑完整，也就是说必须修建在单位格子的边界上并且不能只修建一部分。

 

输入输出格式

输入格式：

文件的第一行包含两个整数n和m。接下来n行每行m个整数，1表示该格子属于狼的领地，2表示属于羊的领地，0表示该格子不是任何一只动物的领地。

 

输出格式：

文件中仅包含一个整数ans，代表篱笆的最短长度。

 

输入输出样例

输入样例#1：

2 2

2 2

1 1

输出样例#1：

2

说明

数据范围

10%的数据 n，m≤3

 

30%的数据 n，m≤20

 

100%的数据 n，m≤100

 

   这个题的本质就是用最少的代价分隔开1和2的联通块，可以考虑用最小割来做。不过建模过程是需要思考的，尽管2->1是一定要有边的，但是0这种格子就不好处理了。因为这种情况可能不是沿0/2的分界线或0/1的分界线，比如

1 1 1
1 0 1
2 0 2
2 2 2

   这时我们在第二行和第三行之间防止栅栏，就只用3块，而且穿过了0和0。那么我们注意到0和0之间没有严格“立场”关系，而我们却可以在两个0之间建栅栏，那么我们给0和0之间双向连为1的边，就能解决这个问题，同样满足了最小割。

   不过，为了把2和1分到两边去，我们要做的是把源点S连给所有2，再把所有1连到汇点T。于是，模型建立大概是这样的：

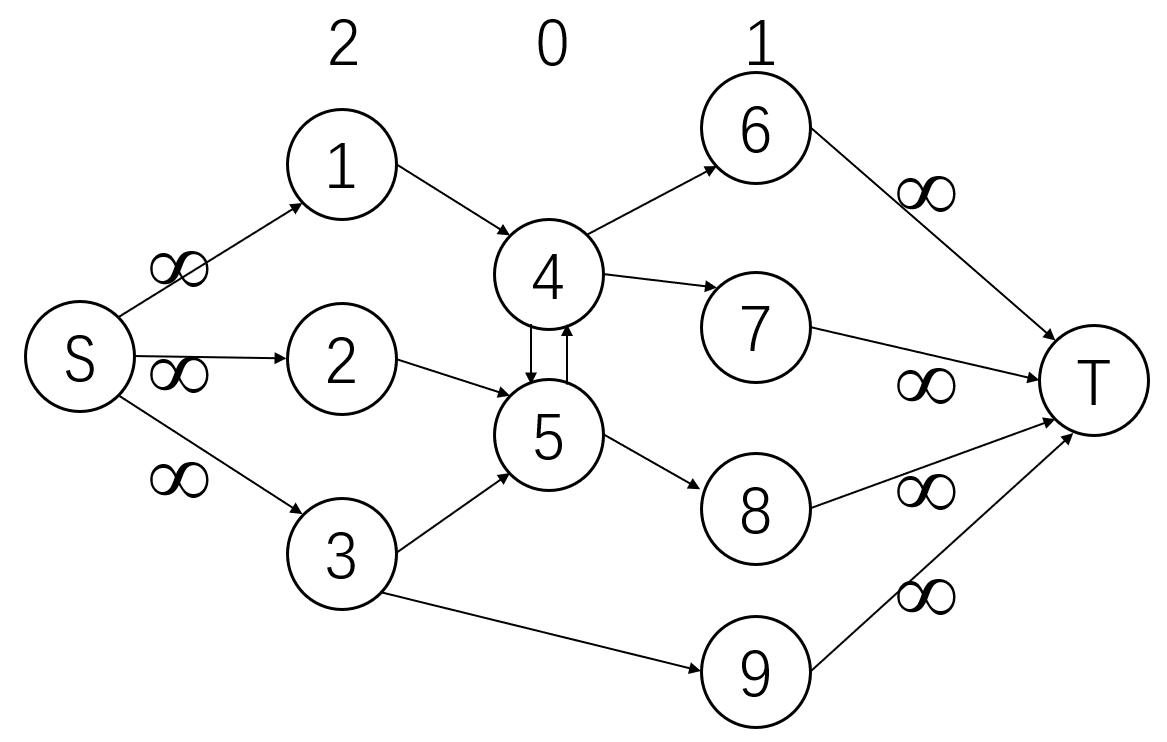
   除了连到源点和汇点的边是∞以外，其余的有箭头的边都是1。而0和0格之间连的是双向边，因此都要有权值（我连了一共4条边，有点浪费）

   最近做最小割的题目有点多，归根结底，问题就是使一个图分成两半，而损失最小。

Code：优雅的isap

#include<cstdio>
#include<cstring>
#define S 0
#define T 55555
struct edge
{
    int n,v;
    int nxt;
    edge(int n,int v,int nxt)
    {
        this->n=n;
        this->v=v;
        this->nxt=nxt;
    }
    edge(int n,int v)
    {
        this->n=n;
        this->v=v;
        nxt=-1;
    }
    edge(){nxt=-1;}
}e[66666];
int head[66666],cnt=-1;
void add(int x,int y,int v)
{
    e[++cnt]=edge(y,v,head[x]);
    head[x]=cnt;
    e[++cnt]=edge(x,0,head[y]);
    head[y]=cnt;
}
int pre[66666],cur[66666];
int n,m,sum=0;
int gap[66666];
void isap()
{
    gap[0]=0x3fffffff;
    int d[66666];
    memset(d,0,sizeof(d));
    int s=S,flag;
    pre[S]=-1;
    for(int i=0;i<=n*m;i++)
        cur[i]=head[i];
    cur[T]=head[T];
    while(d[s]!=T)
    {
        if(s==T)
        {
            int p=s,minn=0x3fffffff;
            while(~pre[p])
            {
                minn=minn<e[pre[p]].v?minn:e[pre[p]].v;
                p=e[pre[p]^1].n;
            }
            sum+=minn;
            p=s;
            while(~pre[p])
            {
                e[pre[p]].v-=minn;
                e[pre[p]^1].v+=minn;
                p=e[pre[p]^1].n;
            }
            s=S;
        }
        flag=0;
        for(int i=cur[s];~i;i=e[i].nxt)
        {
            if(e[i].v>0&&d[e[i].n]+1==d[s])
            {
                flag=1;
                cur[s]=e[i].nxt;
                s=e[i].n;
                pre[s]=i;
                break;
            }
        }
        if(flag==0)//return
        {
            int r=d[s];
            d[s]=T;
            for(int i=head[s];~i;i=e[i].nxt)
                if(e[i].v>0)
                    d[s]=d[s]<d[e[i].n]+1?d[s]:d[e[i].n]+1;
            gap[r]--;
            gap[d[s]]++;
            if(gap[r]==0)
                return;
            cur[s]=head[s];
            if(s==S)
                continue;
            s=e[pre[s]^1].n;
        }
    }
    return;
}
int a[101][101];
bool used[101][101];
int main()
{
    memset(head,-1,sizeof(head));
    memset(a,-1,sizeof(a));
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&a[i][j]);
            if(a[i][j]==1)
                add((i-1)*m+j,T,0x3fffffff);
            if(a[i][j]==2)
                add(S,(i-1)*m+j,0x3fffffff);
            ////
            if(i>1&&a[i][j]==a[i-1][j]&&a[i][j]==0)
            {
                add((i-1)*m+j,(i-2)*m+j,1);
                add((i-2)*m+j,(i-1)*m+j,1);
            }
            if(i>1&&a[i][j]!=a[i-1][j])
            {
                if(a[i][j]==2)
                    add((i-1)*m+j,(i-2)*m+j,1);
                else if(a[i][j]==1)
                    add((i-2)*m+j,(i-1)*m+j,1);
                else
                {
                    if(a[i-1][j]==1)
                        add((i-1)*m+j,(i-2)*m+j,1);
                    else
                        add((i-2)*m+j,(i-1)*m+j,1);
                }
            }

            ////
            if(j>1&&a[i][j]==a[i][j-1]&&a[i][j]==0)
            {
                add((i-1)*m+j,(i-1)*m+j-1,1);
                //add((i-1)*m+j,(i-1)*m+j-1,1);
                add((i-1)*m+j-1,(i-1)*m+j,1);
            }
            if(j>1&&a[i][j]!=a[i][j-1])
            {
                if(a[i][j]==2)
                    add((i-1)*m+j,(i-1)*m+j-1,1);
                else if(a[i][j]==1)
                    add((i-1)*m+j-1,(i-1)*m+j,1);
                else
                {
                    if(a[i][j-1]==1)
                        add((i-1)*m+j,(i-1)*m+j-1,1);
                    else
                        add((i-1)*m+j-1,(i-1)*m+j,1);
                }
            }
            ////
        }
    isap();
    printf("%d\n",sum);
    return 0;
}