洛谷 P2047 [NOI2007]社交网络 题解【最短路】【Floyd】
点击量:268
用floyd解决的最短路计数问题。
题目描述
在社交网络(social network)的研究中,我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题。在一个社交圈子里有n个人,人与人之间有不同程度的关系。我 们将这个关系网络对应到一个n个结点的无向图上,两个不同的人若互相认识,则在他们对应的结点之间连接一条无向边,并附上一个正数权值c,c越小,表示两 个人之间的关系越密切。
我们可以用对应结点之间的最短路长度来衡量两个人s和t之间的关系密切程度,注意到最短路径上的其他结点为s和t的联系提供了某种便利, 即这些结点对于s 和t之间的联系有一定的重要程度。我们可以通过统计经过一个结点v的最短路径的数目来衡量该结点在社交网络中的重要程度。
考虑到两个结点A和B之间可能会有多条最短路径。我们修改重要程度的定义如下:
令Cs,t表示从s到t的不同的最短路的数目,Cs,t(v)表示经过v从s到t的最短路的数目;则定义
$ I(v)=\sum\limits_{s\neq v,t\neq v}\frac{C_{s,t}(v)}{C_{s,t}}$
为结点v在社交网络中的重要程度。
为了使I(v)和Cs,t(v)有意义,我们规定需要处理的社交网络都是连通的无向图,即任意两个结点之间都有一条有限长度的最短路径。
现在给出这样一幅描述社交网络s的加权无向图,请你求出每一个结点的重要程度。
输入输出格式
输入格式:
输入第一行有两个整数,n和m,表示社交网络中结点和无向边的数目。在无向图中,我们将所有结点从1到n进行编号。
接下来m行,每行用三个整数a, b, c描述一条连接结点a和b,权值为c的无向边。注意任意两个结点之间最多有一条无向边相连,无向图中也不会出现自环(即不存在一条无向边的两个端点是相同的结点)。
输出格式:
输出包括n行,每行一个实数,精确到小数点后3位。第i行的实数表示结点i在社交网络中的重要程度。
输入输出样例
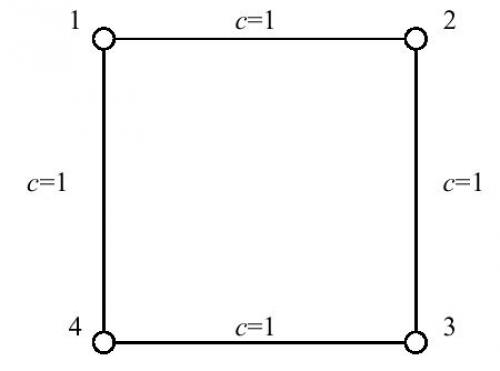
输入样例#1:4 41 2 12 3 13 4 14 1 1输出样例#1:1.0001.0001.0001.000说明
对于1号结点而言,只有2号到4号结点和4号到2号结点的最短路经过1号结点,而2号结点和4号结点之间的最短路又有2条。因而根据定义,1号结点的重要程度计算为1/2+1/2=1。由于图的对称性,其他三个结点的重要程度也都是1。
50%的数据中:n ≤10,m ≤45
100%的数据中:n ≤100,m ≤4 500,任意一条边的权值c是正整数,满足:1 ≤c ≤1 000。
所有数据中保证给出的无向图连通,且任意两个结点之间的最短路径数目不超过10^10。
数据范围是100,因此$ N^3$的复杂度是可以过的,洛谷神鸡轻轻松松$ N^4$,一开始我是最短路计数用floyd打的,然后统计作为通过点的计数写的dfs,结果dfs会被网格图卡。。。现在终于知道dfs一张图不是$ N^2$了,还有一种叫网格图的东西,以后拿去出题害人。
首先统计最短路用floyd,就是根据乘法原理。当i到k是最短路同时k到j是最短路,那么i到j这条最短路的方案就是前两种方案之积。当最短路更新时,之前统计的方案清零,重新计算当前状态下的最短路。(第一次floyd)
统计作为通过点的计数也可以用floyd(第二次floyd),只要判断f[i][k]+f[k][j]刚好等于f[i][j],就说明k在i到j的最短路上(由三角形不等式),这样和上面同理,直接把方案数加上两边方案数的乘积。因为此时的最短路状态不会再被更新了。
其实这类题有更好的利用SPFA等最短路算法的做法,可以做一下最短路计数,数据范围比较大。
Code:
#include<cstdio>
#include<cstring>
struct edge//前向星
{
int n,v;
int nxt;
edge(int n,int v,int nxt)
{
this->n=n;
this->v=v;
this->nxt=nxt;
}
edge(int n,int v)
{
this->n=n;
this->v=v;
nxt=-1;
}
edge()
{
nxt=-1;
}
}e[42000];
int f[120][120],num=-1;
int head[120];
void add(int from,int to,int v)
{
e[++num]=edge(to,v,head[from]);
head[from]=num;
}
long long cnt[120][120];//i到j的最短路有多少条
long long cnt1[120][120][120];//经过i,从j到k的最短路有多少条
bool used[120];
long long sum=0;
int pre[120];
int n;
void solve(int x)//最后求解
{
double ans=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i!=x&&j!=x&&i!=j)
ans+=double(cnt1[x][i][j]*1.0/(cnt[i][j]*1.0));
printf("%.3lf\n",ans);
}
int main()
{
memset(head,-1,sizeof(head));
memset(cnt1,0,sizeof(cnt1));
memset(f,0x3f,sizeof(f));
int m,u,v,w;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
f[i][i]=0;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,w);
f[u][v]=w;
f[v][u]=w;
cnt[u][v]=1;
cnt[v][u]=1;
}
//floyd
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(f[i][j]>=f[i][k]+f[k][j]&&i!=j&&i!=k&&k!=j)
{
if(i==1&&j==2)
{
int r;
r=1;
}
if(f[i][j]>f[i][k]+f[k][j])
cnt[i][j]=cnt[i][k]*cnt[k][j];
else
cnt[i][j]+=cnt[i][k]*cnt[k][j];
f[i][j]=f[i][k]+f[k][j];
}
//floyd2
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(f[i][j]==f[i][k]+f[k][j]&&i!=j&&i!=k&&k!=j)
cnt1[k][i][j]=cnt[i][k]*cnt[k][j];
for(int i=1;i<=n;i++)
solve(i);
return 0;
}


… [Trackback]
[…] Find More on that Topic: wjyyy.top/660.html […]
… [Trackback]
[…] Find More Information here to that Topic: wjyyy.top/660.html […]
… [Trackback]
[…] Read More to that Topic: wjyyy.top/660.html […]
… [Trackback]
[…] Info on that Topic: wjyyy.top/660.html […]