凸包 旋转卡壳 学习笔记【计算几何】

点击量：409

    以前的凸包可能是死记硬背的……不过现在算理解了。

凸包

定义

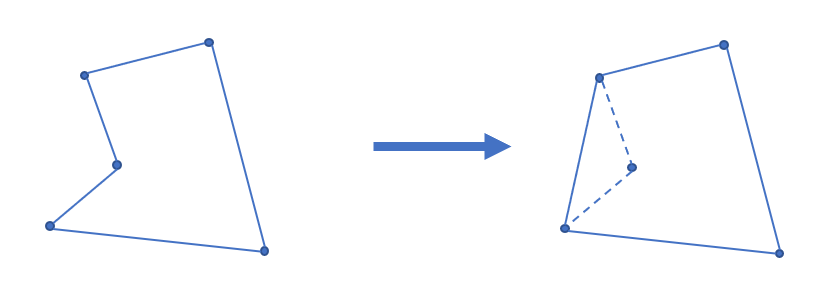
    凸包就是求一个周长最小的，并且能包围所有给定点的多边形。当多边形表面存在凹陷时，根据三角不等式\(\left\{\begin{matrix}a+b>c\\ b+c>a\\ a+c>b\end{matrix}\right.\)，一定没有直接把最短那条边连起来优。

性质

    如果按逆时针方向看，凸包上每两条相邻的边都是向左拐的。比如说，与边\(\vec{a_i}\)顺时针方向相邻的是边\(\vec{a_{i+1}}\)，那么对于任意\(i\in[1,n)\)（\(n\)为凸包上点的个数）有\(\vec{a_i}\times \vec{a_{i+1}}>0,\vec{a_n}\times \vec{a_1}>0\)。因为用右手从\(\vec{a_i}\)的方向顺小于平角的一边握向\(\vec{a_{i+1}}\)，大拇指总会指向外边。

求法

    因为总是向左拐，所以可以用一个单调栈来维护，如果发现栈顶下的点、栈顶、即将进栈的点（有序）构成的夹角变成向右拐了，则弹出栈顶。接着返回上一步，继续检查栈顶。但是我们需要一个枚举顺序。

    首先把所有点按照横坐标为第一关键字，纵坐标为第二关键字排序。此时可以保证，数组中最小的元素和最大的元素一定都在凸包内。那么我们先按顺序枚举出下凸壳，然后逆序枚举出上凸壳。

    最后不要忘了把最小的元素与栈顶进行比较，以保证最后一段也是凸壳。

代码

std::sort(p+1,p+1+n);
stk[++tp]=1;
for(int i=2;i<=n;++i)
{
    while(tp>1&&(p[stk[tp]]-p[stk[tp-1]])*(p[i]-p[stk[tp]])<=0)
        used[stk[tp--]]=0;
    used[i]=1;
    stk[++tp]=i;
}
int qaq=tp;
for(int i=n-1;i>0;--i)
    if(!used[i])
    {
        while(tp>qaq&&(p[stk[tp]]-p[stk[tp-1]])*(p[i]-p[stk[tp]])<=0)
            used[stk[tp--]]=0;
        used[i]=1;
        stk[++tp]=i;
    }
for(int i=1;i<=tp;++i)
    h[i]=p[stk[i]];

    最后\(h\)数组中存的就是凸包了。（下标\(1\)和\(tp\)存的是同一个点）

例题

UVA 11626 Convex Hull

洛谷 P2742 圈奶牛

这篇文章会更新近期做的一些计算几何题目。

旋转卡壳

跟我一起读\[\text{xu}\grave{\text a}\text n\ \text{zhu}\check{\text a}\text n\ \text{qi}\check{\text a}\ \text{qia}\grave{\text o}\\
\huge 旋\ 转\ 卡\ 壳\]

我也不知道该怎么读。

前言

    刚学旋转卡壳时，是看到了一句话：“同时旋转两条平行线直到其中一条和多边形的一条边重合”。那不就是旋转到夹角较小的那一条边上去吗？

    \(\angle 1<\angle 2\)，那么我们把平行线逆时针旋转过\(\angle 1\)的大小，就可以和多边形的一边重合了。

    于是就出现了这样的代码：

/***vct结构体内部***/
friend db operator ^(vct a,vct b)//求夹角
{
    db tmp=a.x*b.x+a.y*b.y;
    tmp/=a.dis();
    tmp/=b.dis();
    return fabs(acos(tmp));
}

/***主函数中***/
while(t2<tp)
{
    db d1=t^(h[t1+1]-h[t1]);//夹角1
    db d2=t_^(h[t2+1]-h[t2]);//夹角2
    if(d1<d2)
    {
        ++t1;
        t.rot(d1);
        t_.rot(d1);
    }
    else
    {
        ++t2;
        t.rot(d2);
        t_.rot(d2);
    }
    db tmp=(h[t1]-h[t2]).dis();
    ans=ans>tmp?ans:tmp;
}

    然而这样会产生较大的精度误差，显然不是计算几何想要的。

凸多边形的切线

    如果一条直线与凸多边形有交点，并且整个凸多边形都在这条直线的一侧，那么这条直线就是该凸多边形的一条切线。

对踵点

    如果过凸多边形上两点作一对平行线，使得整个多边形都在这两条线之间，那么这两个点被称为一对对踵点。

凸多边形的直径

    即凸多边形上任意两个点之间距离的最大值。直径一定会在对踵点中产生，如果两个点不是对踵点，那么两个点中一定可以让一个点向另一个点的对踵点方向移动使得距离更大。并且点与点之间的距离可以体现为线与线之间的距离，在非对踵点之间构造平行线，一定没有在对踵点构造平行线优，这一点可以通过平移看出。

旋转卡壳

    为了减小误差（上面那个傻乎乎的方法误差就比较大，并方便计算，我们求出每一条边的对踵点。通过上面的图可以看出，边的对踵点同时是这两个点的对踵点，因此并没有遗漏。

    同时，通过边来求，可以很好地运用叉积的计算，减小了误差。

    对于最下面这条边来说，对于上面四个顶点，他们分别与这条边构成了四个同底不同高的三角形，而三角形面积可以用叉积算出来，三角形的面积此时也就反映了点到直线的距离了。由于面积是单峰的，那么对单独一条边的对踵点，我们可以用三分来求，对于所有边，我们可以用two-pointer来\(O(n)\)求出。因为随着边在逆时针枚举，它的对踵点\(T\)也在逆时针移动。

补充：对于三角形面积

因为\[\left\{\begin{matrix}\vec{AB}\times\vec{AC}=|AB||AC|\sin\theta,\\ S_{\triangle ABC}=\frac 12 |AB||AC|\sin \theta=\frac 12 |BC|h\end{matrix}\right.(\theta=\angle BAC)\]，两式联立得\(h=\frac{\vec{AB}\times\vec{AC}}{|BC|}\)。

    因此可以用旋转卡壳来求凸多边形直径。

步骤

    首先求出凸包，目的是把所有点按逆时针排序。然后枚举逆时针边，定义\(T\)为当前的对踵点，若\(T\)逆时针变动能增大到当前边的距离则改变\(T\)，直到继续改变会导致距离减小为止。每次求出边（设为\(AB\)）的对踵点\(T_i\)后，分别用\(|AT_i|,|BT_i|\)来更新答案，即凸多边形的直径。

代码

db dis(vct a,vct b,vct x)//求出x到ab的距离
{
    return fabs((a-x)*(b-x)/(a-b).dis());
}
int t=1;
db ans=0.0;
for(int i=1;i<tp;++i)
{
    while(dis(h[i],h[i+1],h[t])<=dis(h[i],h[i+1],h[t+1]))
        t=t%(tp-1)+1;
    ans=std::max(ans,std::max((h[i]-h[t]).dis(),(h[i+1]-h[t]).dis()));//这里的dis是向量的模长
}

例题

洛谷 P1452 Beauty Contest

UVA10173 Smallest Bounding Rectangle \(O(n^2)\)求最小覆盖矩形

洛谷 P3187 [HNOI2007]最小矩形覆盖 \(O(n\log n)\)求最小覆盖矩形并输出矩形顶点（bzoj有spj）