洛谷 P2114 [NOI2014]起床困难综合症 题解【贪心】【二进制】

点击量：21

   位运算的奇技淫巧*

目录

题目描述

21世纪，许多人得了一种奇怪的病：起床困难综合症，其临床表现为：起床难，起床后精神不佳。作为一名青春阳光好少年，atm一直坚持与起床困难综合症作斗争。通过研究相关文献，他找到了该病的发病原因： 在深邃的太平洋海底中，出现了一条名为drd的巨龙，它掌握着睡眠之精髓，能随意延长大家的睡眠时间。 正是由于drd的活动，起床困难综合症愈演愈烈， 以惊人的速度在世界上传播。为了彻底消灭这种病，atm决定前往海底，消灭这条恶龙。历经千辛万苦，atm终于来到了drd所在的地方，准备与其展开艰苦卓绝的战斗。drd有着十分特殊的技能，他的防御战线能够使用一定的运算来改变他受到的伤害。具体说来，drd的防御战线由n扇防御门组成。每扇防御门包括一个运算op和一个参数t，其中运算一定是OR,XOR,AND中的一种，参数则一定为非负整数。如果还未通过防御门时攻击力为x，则其通过这扇防御门后攻击力将变为x op t。最终drd受到的伤害为对方初始攻击力x依次经过所有n扇防御门后转变得到的攻击力。

 

由于atm水平有限，他的初始攻击力只能为0到m之间的一个整数（即他的初始攻击力只能在 0, 1, … , m中任选，但在通过防御门之后的攻击力不受m的限制）。为了节省体力，他希望通过选择合适的初始攻击力使得他的攻击能让drd受到最大的伤害，请你帮他计算一下，他的一次攻击最多能使drd受到多少伤害。

 

输入输出格式

输入格式：

输入文件的第 1 行包含 2 个整数，依次为n, m，表示 drd 有n扇防御门，atm 的初始攻击力为0到m之间的整数。

 

接下来n行，依次表示每一扇防御门。每行包括一个字符串op和一个非负整数t，两者由一个空格隔开，且op在前，t在后，op表示该防御门所对应的操作，t表示对应的参数。

 

输出格式：

输出一行一个整数，表示atm的一次攻击最多使drd受到多少伤害。

 

输入输出样例

输入样例#1：

3 10

AND 5

OR 6

XOR 7

输出样例#1：

1

说明

【样例说明】

atm可以选择的初始攻击力为 0,1, … ,10。

假设初始攻击力为 4，最终攻击力经过了如下计算

4 AND 5 = 4

4 OR 6 = 6

6 XOR 7 = 1

类似的，我们可以计算出初始攻击力为 1,3,5,7,9 时最终攻击力为 0，初始攻击力为 0,2,4,6,8,10 时最终攻击力为 1，因此atm的一次攻击最多使drd受到的伤害值为1。

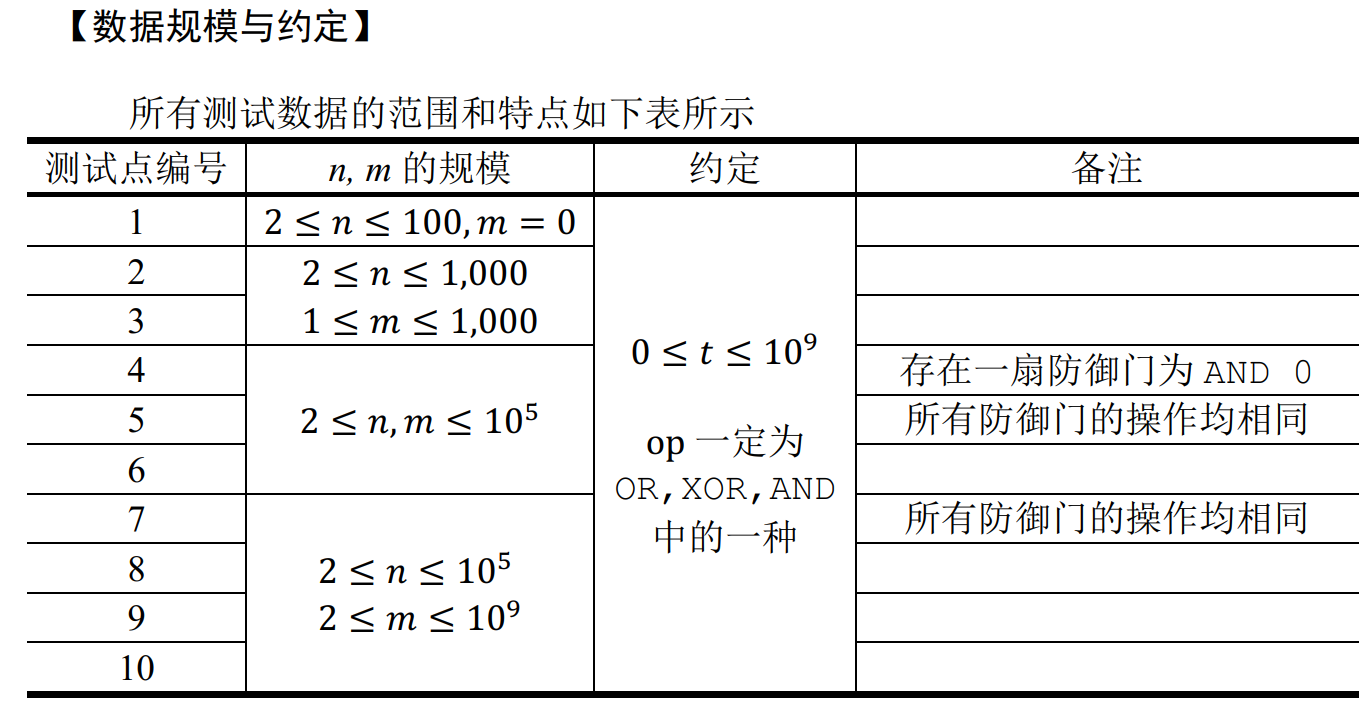
【数据规模与约定】

【 运算解释】
在本题中， 选手需要先将数字变换为二进制后再进行计算。 如果操作的两个数二进制长度不同，则在前补 0 至相同长度。

 

OR 为按位或运算， 处理两个长度相同的二进制数， 两个相应的二进制位中只要有一个为 1， 则该位的结果值为 1， 否则为 0。 XOR 为按位异或运算， 对等长二进制模式或二进制数的每一位执行逻辑异或操作。 如果两个相应的二进制位不同（相异）， 则该位的结果值为 1， 否则该位为 0。 AND 为按位与运算， 处理两个长度相同的二进制数， 两个相应的二进制位都为 1， 该位的结果值才为 1，否则为 0。

例如，我们将十进制数 5 与十进制数 3 分别进行 OR， XOR 与 AND 运算，可以得到如下结果：

   0101 (十进制 5)     0101 (十进制 5)     0101 (十进制 5)
OR 0011 (十进制 3) XOR 0011 (十进制 3) AND 0011 (十进制 3)
 = 0111 (十进制 7)   = 0110 (十进制 6)   = 0001 (十进制 1)

题解：

   首先，测试点1，2，3的30分是送的，枚举m模拟就可以。对于剩下m超过10000的点，就不好直接做了。

   不过对二进制来说，我们可以知道当第k位为0或1时，它经过n次操作的结果是多少，因为每次操作的第k位是确定的。所以通过000000…000和111111…111来进行这些操作，得到第k位的结果就分别是当第k位为0或1时的结果了。

   这时我们从大到小枚举。如果第i位的结果为0，那么就不选，如果第i位结果为1，判断原数在这一位是由0还是1变过来的。如果0可以变过来，就直接选，答案位或1，对原数没有影响；如果0,1都可以选，果断选0，原数保持不变，答案位或1，根据贪心，原数越小，后面的选取空间越大；如果只能取1，判断取之后原数位或1会不会超过m，如果不超过，把原数这一位位或1，答案也位或1，因为根据贪心，选越大的越好。

   这个题其实就是计算了各个位上的情况，也就是知道了这一位取0与取1的结果，这样就用0x7fffffff和0来看每一位取1或取0，最后贪心选最优解且不超过m。

Code：

#include<cstdio>
#include<cstring>
int main()
{
    int a=0,b=0x7fffffff;
    int n,m,t;
    char op[10];
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",op);
        scanf("%d",&t);
        if(op[0]=='A')
            a&=t,b&=t;
        else if(op[0]=='O')
            a|=t,b|=t;
        else
            a^=t,b^=t;
    }
    int ans=0,ori=0;//答案/原数
    for(int i=30;i>=0;--i)
    {
        if((a&(1<<i))>0)//0直接选
            ans|=(1<<i);
        else if((b&(1<<i))>0&&(ori|(1<<i))<=m)//1要对原数进行判断
        {
            ans|=(1<<i);
            ori|=(1<<i);
        }

    }
    printf("%d\n",ans);
    return 0;
}