计算几何 学习笔记合集【凸包】【旋转卡壳】【半平面交】
点击量:849
引言
计算几何对于很多刚接触OI的同学们是不会涉及的,当逐步进入省选范畴之后,计算几何的应用就非常广了。
本文同 洛谷日报 #142。
你需要知道?
在学习计算几何(至少是这篇文章)之前,你需要了解以下这些东西:
- 平面直角坐标系
- 向量及其运算
- 三角剖分求面积
平面直角坐标系
平面直角坐标系就是笛卡尔坐标系,这一部分会在人教版七年级数学中系统地学习。
在这篇文章中,我们会经常用到坐标表示,包括下面的向量。同时,我们的点和向量都是通过坐标来保存的。
向量及其运算
向量
向量是既有大小又有方向的量,可以用一个带有箭头的线段表示。
如果一个向量的起点是点 $A$,终点是点 $B$,那么这个向量可以被表示为 $\overrightarrow{AB}$,或者用一个小写英文字母表示为 $\vec{a}$ 或 $\mathbf{a}$(教科书上加粗时也是斜体)。
向量具有平移不变性,对于任意一个向量,都可以把它的起点平移到原点。因此我们可以在坐标系中用一对有序实数对来表示向量,也就是这个向量起点为原点时终点的坐标 $(x,y)$。
向量的模
模就是模长,向量的模就是向量的长度。表示为 $|\vec{a}|$,对于 $\vec{a}=(x,y),\left|\vec{a}\right|=\sqrt{x^2+y^2}$。
相反向量
如果两个向量大小相等,方向相反,那么这两个向量互为相反向量,$\vec{a}$ 的相反向量表示为 $-\vec{a}$,$\left|\vec{a}\right|=-\vec{a}$。对于 $\vec{a}=(x,y),-\vec{a}=(-x,-y)$。
垂直向量
如果两个向量所在的直线互相垂直,那么这两个向量互称垂直向量,表示为 $\vec{a}\bot\vec{b}$。
共线向量
如果两个向量所在的直线互相平行,那么这两个向量互为共线向量,表示为 $\vec{a}|\vec{b}$。因为两向量平行,所以平移其中一个向量,总能和另一个向量共线。
向量的加减
前面提到了向量具有平移不变性,那么 $\vec{a}+\vec{b}$ 就相当于把向量 $\vec{a},\vec{b}$ 首尾相接(假设 $\vec{a}$ 的首接在 $\vec{b}$ 的尾),此时 $\vec{a}$ 的尾指向 $\vec{b}$ 的首就是相加后的向量。对于 $\vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2)$,$\vec{a}+\vec{b}=(x_1+x_2,y_1+y_2)$。

向量的减法实际上是一个向量加上另一个向量的相反向量,也就是 $\vec{a}-\vec{b}=\vec{a}+\left(-\vec{b}\right)$,可以先把 $\vec{b}$ 向量变成 $-\vec{b}$,然后再进行加法计算。$\vec{a}-\vec{b}=(x_1-x_2,y_1-y_2)$。

向量的加减法具有交换律。
零向量
零向量的模长为 $0$ ,方向任意,它与任何一个向量都共线,但在高中数学中不认为它与任何一个向量都垂直。坐标为 $(0,0)$。
向量的数乘
向量的数乘实际上是对向量进行放缩。数乘的形式是 $\lambda\vec{a}$,其中常数 $\lambda\in\mathbb{R}$ 是对向量放缩的程度,可正可负可为零。数乘不改变向量的方向,因此 $\vec{a}|\lambda\vec{a}$。对于 $\vec{a}=(x,y),\lambda\vec{a}=(\lambda x,\lambda y)$。
向量的数量积
向量的数量积,也叫点积、内积,几何意义为一个向量在另一个向量上的投影再乘上第二个向量的模长。$\vec{a}$ 与 $\vec{b}$ 的数量积表示为 $\vec{a}\cdot\vec{b}$,是一个实数。计算式为 $\vec{a}\cdot\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\cos\theta(\theta=\left<\vec{a},\vec{b}\right>)$($\theta$ 表示 $\vec{a},\vec{b}$ 的夹角)。引入坐标后,通过三角恒等变换的推导,对于 $\vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2)$,$\vec{a}\cdot\vec{b}=x_1x_2+y_1y_2$。
- 如果两个向量同向(共线),那么它们的数量积为他们的模长之积。
- 如果两个向量夹角 $<90^\circ$,那么它们的数量积为正。
- 如果两个向量夹角 $=90^\circ$,那么他们的数量积为 $0$,因为 $\cos 90^\circ=0$。
- 如果两个向量夹角 $>90^\circ$,那么它们的数量积为负。
- 如果两个向量反向(共线),那么它们的数量积为他们的模长之积的相反数。
由向量的数量积可以判断它们的夹角和投影。向量的数量积具有交换律。
向量的外积
向量的外积,也叫叉积,几何意义是两向量由平行四边形法则围成的面积。外积是一个向量,垂直于原来两个向量所在的平面。对于 $\vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2)$,$\vec{a}\times\vec{b}$ 的方向就要用右手从$\vec{a}$沿着不大于平角的方向旋转,大拇指的方向就是外积的方向。如果外积方向朝外,那么值为正,否则值为负。计算式为 $\vec{a}\times\vec{b}=|\vec{a}||\vec{b}|\sin\theta=x_1y_2-x_2y_1$。因为有谁转向谁的区别,所以外积没有交换律。
$\vec a\times \vec b$ 的正负也可以理解为,把 $\vec a$ 顺时针方向转到 $\vec b$ 的方向,夹角为 $\theta$。当 $0\le\theta<\pi$ 时值为正;当 $\pi\le\theta<2\pi$ 时值为负。
- 如果 $\vec{a}|\vec{b}$,那么由 $\sin 0^\circ=\sin 180^\circ=0,\vec{a}\times\vec{b}=\vec{0}$,得到的数字结果也是$0$。
- 如果 $\vec{b}$ 的终点在 $\vec{a}$ 的左侧(假设已经共起点),那么 $\vec{a}\times \vec{b}>0$,$\vec{a}$ 握向 $\vec{b}$转过的角逆时针不超过 $180^\circ$,结果为正。
- 如果 $\vec{b}$ 的终点在 $\vec{a}$ 的右侧,那么 $\vec{a}\times \vec{b}<0$,$\vec{a}$ 握向 $\vec{b}$ 转过的角逆时针超过了 $180^\circ$,或者说顺时针不超过 $180^\circ$,大拇指朝内,结果为负。
由向量外积可以判断两向量的旋转关系,同时可以方便地求出点到直线的距离。分别会用于下面的凸包和旋转卡壳。
一般情况下我们储存点就会把它放在向量中,用向量 $\overrightarrow{OA}$ 来表示 $A$ 这个点。因此下文的 $A\times B$ 就表示向量 $\overrightarrow{OA}$ 与向量 $\overrightarrow{OB}$ 的叉积。
线段交点
upd on 2019.3.12
根据面积我们可以求出两线段交点。
我们对于两个线段 $AB,CD$,可以通过面积和相似来求出交点 $O$ 的坐标。因为 $A$ 的坐标已知,实际上是通过求出 $\overrightarrow{AO}$ 来确定 $O$ 的坐标。
我们根据上面的叉积公式求面积,得到 $S_{\triangle ACD}=\frac{\overrightarrow{AD}\times\overrightarrow{AC}}2,S_{\triangle BCD}=\frac{\overrightarrow{BC}\times \overrightarrow{BD}}2$。
再作垂线 $AE\bot CD,BF\bot CD$,$S_{\triangle ACD}=\frac {|CD|\times |AE|}2,S_{\triangle BCD}=\frac {|CD|\times |BF|}2$。则 $\frac{|AE|}{|BF|}=\frac{S_{\triangle ACD}}{S_{\triangle BCD}}$。
此时 $\triangle AEO\backsim\triangle BFO$,得到 $\frac{|AE|}{|BF|}=\frac{|AO|}{|BO|}$。

又因为 $\overrightarrow{AO}=\frac{|AO|}{|AB|}\cdot \overrightarrow{AB}=\frac{|AO|}{|AO|+|BO|}\cdot \overrightarrow{AB}$,令原点为 $O’$,则 $\overrightarrow{O’O}=\overrightarrow{O’A}+\overrightarrow{AO}$,$\overrightarrow{O’O}$ 的坐标即为 $O$ 的坐标。
向量旋转
upd on 2019.3.1
这个知识点虽然在这篇文章里没有应用,但是是计算几何的基本操作技巧。
设 $\vec a=(x,y)$ ,倾角为 $\theta$ ,长度为 $l=\sqrt{x^2+y^2}$。则 $x=l\cos \theta,y=l\sin\theta$。令其顺时针旋转 $\alpha$ 度角,得到向量 $\vec b=(l\cos(\theta+\alpha),l\sin(\theta+\alpha))$。

由三角恒等变换得,
$$
\vec{b}=(l(\cos\theta\cos\alpha-\sin\theta\sin\alpha),l(\sin\theta\cos\alpha+\cos\theta\sin\alpha))
$$
化简,去括号
$$
\vec b=(l\cos\theta\cos\alpha-l\sin\theta\sin\alpha,l\sin\theta\cos\alpha+l\cos\theta\sin\alpha)
$$
把上面的 $x,y$ 代回来得
$$
\vec b=(x\cos\alpha-y\sin\alpha,y\cos\alpha+x\sin\alpha)
$$
即使不知道三角恒等变换,这个式子也很容易记下来。
三角剖分求面积
三角剖分可以用来求任意多边形的面积。
我们只需要知道一个多边形的各个连续顶点分别在哪里即可。
上面提到了向量的叉积是表示的是有向面积,方向用正负表示,此时正负就派上用场了。
我们如果把相邻每两个顶点与原点构成的向量的叉积的数值的一半依次累加起来,就能得到多边形的面积。如下图:红色面积表示负的,蓝色面积表示正的。
$$S_{ABCDEF}=\overrightarrow{OA}\times \overrightarrow{OB}+\overrightarrow{OB}\times \overrightarrow{OC}+\dots +\overrightarrow{OF}\times \overrightarrow{OA}$$
首先计算 $\overrightarrow{OA}\times \overrightarrow{OB}$,得到负的面积 $-S_{\triangle OAB}$,在图上表示为红色部分;然后计算 $S_{\triangle OBC}$,此时在图上表示为抵消 $-S_{\triangle OBP}$,并额外加上正的 $S_{\triangle PBC}$。

然后依次进行下去
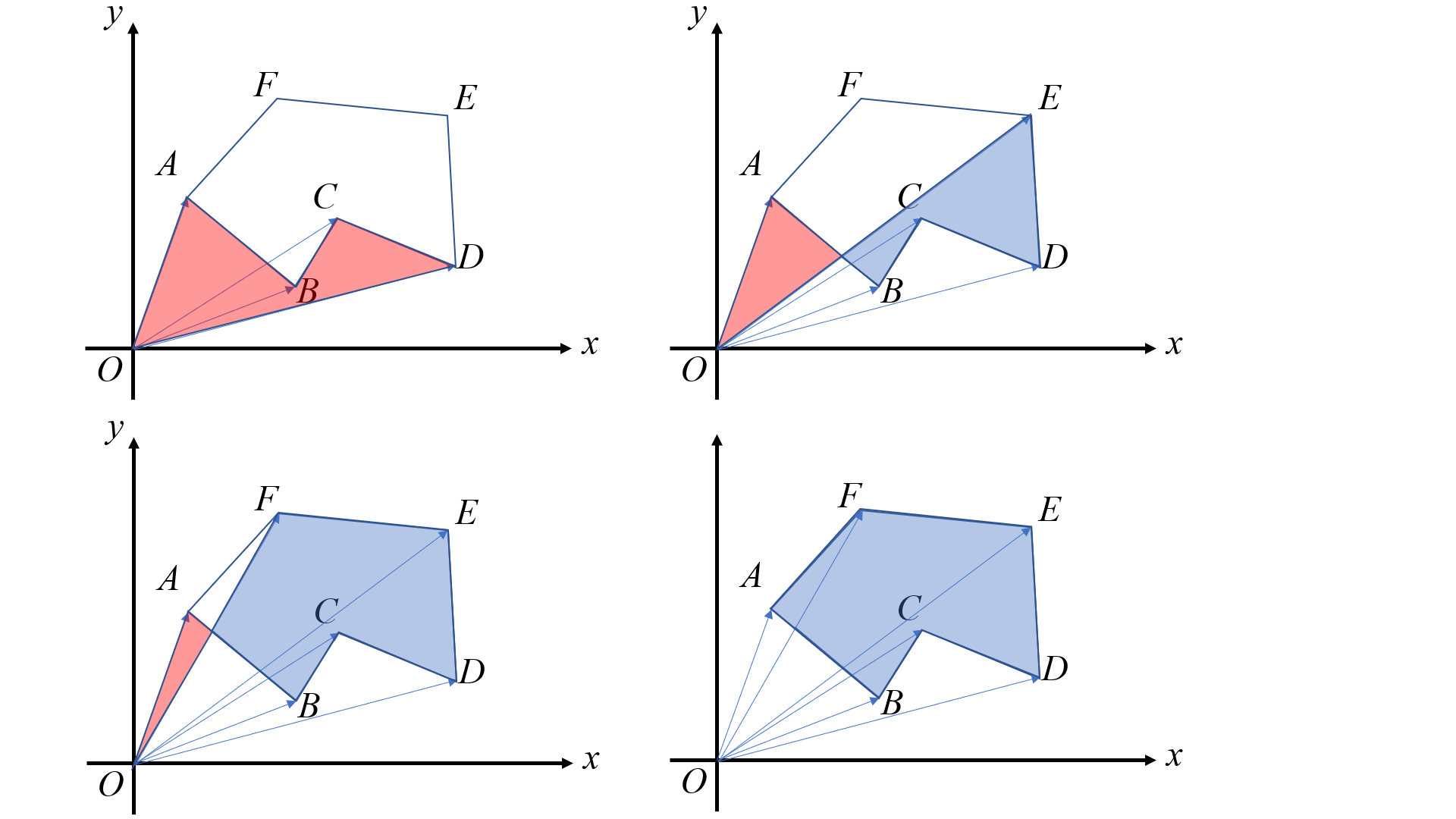
可以看出,多边形外部出现过的红色总会被消掉,因为多边形是闭合的。当出现了一条相对原点向右的边时,则之后必然会出现一条相对原点向左的边来封闭这个多边形。
如果原点在多边形内部就更好理解了。多边形凹的部分会被”拐回来的部分“给减掉,剩下的部分都可以直接相加。
最终对于 $n$ 边形 $A_1A_2\dots A_n$,面积计算公式就是 $S=x_ny_1-y_nx_1+\sum_{i=1}^{n-1}(x_iy_{i+1}-y_ix_{i+1})$。
当用向量存点时,计算可以用相邻向量叉积之和,$S=A_n\times A_1+\sum_{i=1}^{n-1}A_i\times A_{i+1}$。
凸包
定义
凸包就是求一个周长最小的,并且能包围所有给定点的多边形。当多边形表面存在凹陷时,根据三角不等式 $\left\{\begin{matrix}a+b>c\\ b+c>a\\ a+c>b\end{matrix}\right.$,一定没有直接把最短那条边连起来优。
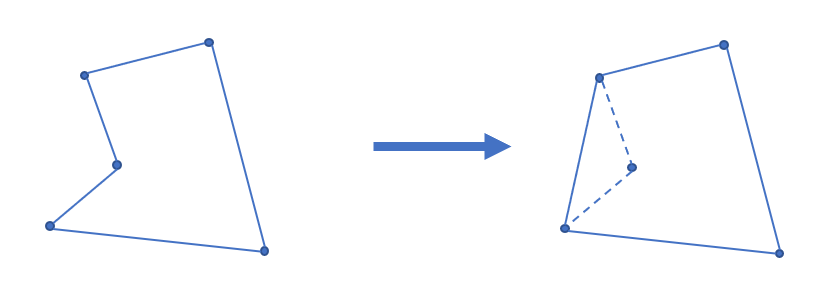
性质
如果按逆时针方向看,凸包上每两条相邻的边都是向左拐的。比如说,与边 $\vec{a}_i$ 顺时针方向相邻的是边 $\vec{a}_{i+1}$,那么对于任意 $i\in[1,n)$( $n$ 为凸包上点的个数)有 $\vec{a}_i\times \vec{a}_{i+1}>0,\vec{a}_n\times \vec{a}_1>0$。因为用右手从 $\vec{a}_i$ 的方向顺小于平角的一边握向 $\vec{a}_{i+1}$,大拇指总会指向外边。
求法
首先把所有点以横坐标为第一关键字,纵坐标为第二关键字排序。
显然排序后最小的元素和最大的元素一定在凸包上。而且因为是凸多边形,我们如果从一个点出发逆时针走,轨迹总是 “左拐” 的,一旦出现右拐,就说明这一段不在凸包上。因此我们可以用一个单调栈来维护上下凸壳。
因为从左向右看,上下凸壳所旋转的方向不同,为了让单调栈起作用,我们首先升序枚举求出下凸壳,然后降序求出上凸壳。
求凸壳时,一旦发现即将进栈的点($P$)和栈顶的两个点($S_1,S_2$,其中 $S_1$ 为栈顶 )行进的方向向右旋转,即叉积小于 $0$:$\overrightarrow{S_2S_1}\times \overrightarrow{S_1P}<0$,则弹出栈顶,回到上一步,继续检测,直到 $\overrightarrow{S_2S_1}\times \overrightarrow{S_1P}\ge 0$ 或者栈内仅剩一个元素为止。
通常情况下不需要保留位于凸包边上的点,因此上面一段中 $\overrightarrow{S_2S_1}\times \overrightarrow{S_1P}<0$ 这个条件中的 “$<$” 可以视情况改为 $\le$,同时后面一个条件应改为 $>$。
最后不要忘了把最小的元素与栈顶进行比较,以保证最后一段也是凸壳。
时间复杂度 $O(n\log n)$。
代码
std::sort(p+1,p+1+n);
stk[++tp]=1;
for(int i=2;i<=n;++i)
{
while(tp>1&&(p[stk[tp]]-p[stk[tp-1]])*(p[i]-p[stk[tp]])<=0)
used[stk[tp--]]=0;
used[i]=1;
stk[++tp]=i;
}
int qaq=tp;
for(int i=n-1;i>0;--i)
if(!used[i])
{
while(tp>qaq&&(p[stk[tp]]-p[stk[tp-1]])*(p[i]-p[stk[tp]])<=0)
used[stk[tp--]]=0;
used[i]=1;
stk[++tp]=i;
}
for(int i=1;i<=tp;++i)
h[i]=p[stk[i]];
最后$h$数组中存的就是凸包了。(下标$1$和$tp$存的是同一个点)
练习
旋转卡壳
跟我一起读
$$\text{xu}\acute{\text a}\text n\ \text{zhu}\check{\text a}\text n\ \text{k}\check{\text a}\ \text{k}\acute{\text e}$$
$$\huge\text{ 旋 转 卡 壳}$$
我也不知道该怎么读。这个词一共有$2^4=16$种读法。
前言
Warning:前言部分仅供引入,严禁参考。
刚学旋转卡壳时,是看到了一句话:“同时旋转两条平行线直到其中一条和多边形的一条边重合”。那不就是旋转到夹角较小的那一条边上去吗?

$\angle 1<\angle 2$,那么我们把平行线逆时针旋转过 $\angle 1$ 的大小,就可以和多边形的一边重合了。
于是就出现了这样的代码:
/***vct结构体内部***/
friend db operator ^(vct a,vct b)//求夹角
{
db tmp=a.x*b.x+a.y*b.y;
tmp/=a.dis();
tmp/=b.dis();
return fabs(acos(tmp));
}
/***主函数中***/
while(t2<tp)
{
db d1=t^(h[t1+1]-h[t1]);//夹角1
db d2=t_^(h[t2+1]-h[t2]);//夹角2
if(d1<d2)
{
++t1;
t.rot(d1);
t_.rot(d1);
}
else
{
++t2;
t.rot(d2);
t_.rot(d2);
}
db tmp=(h[t1]-h[t2]).dis();
ans=ans>tmp?ans:tmp;
}
然而这样会产生较大的精度误差,显然不是计算几何想要的。
凸多边形的切线
如果一条直线与凸多边形有交点,并且整个凸多边形都在这条直线的一侧,那么这条直线就是该凸多边形的一条切线。
对踵点
如果过凸多边形上两点作一对平行线,使得整个多边形都在这两条线之间,那么这两个点被称为一对对踵点。
凸多边形的直径
即凸多边形上任意两个点之间距离的最大值。直径一定会在对踵点中产生,如果两个点不是对踵点,那么两个点中一定可以让一个点向另一个点的对踵点方向移动使得距离更大。并且点与点之间的距离可以体现为线与线之间的距离,在非对踵点之间构造平行线,一定没有在对踵点构造平行线优,这一点可以通过平移看出。
旋转卡壳
这是一张比较标致的动图,生动地体现了旋转卡壳的过程,NOIWC2017中的《膜你抄》中也用了这张图。


为了减小误差(上面那个傻乎乎的方法误差就比较大,并方便计算,我们求出每一条边的对踵点。通过上面的图可以看出,边的对踵点同时是这两个点的对踵点,因此并没有遗漏。
同时,通过边来求,可以很好地运用叉积的计算,减小了误差。

对于最下面这条边来说,对于上面四个顶点,他们分别与这条边构成了四个同底不同高的三角形,而三角形面积可以用叉积算出来,三角形的面积此时也就反映了点到直线的距离了。由于面积是单峰的,那么对单独一条边的对踵点,我们可以用三分来求,对于所有边,我们可以用two-pointer来 $O(n)$ 求出。因为随着边在逆时针枚举,它的对踵点$T$也在逆时针移动。
补充:对于三角形面积
因为
$$\left\{\begin{matrix}\vec{AB}\times\vec{AC}&=&|AB||AC|\sin\theta,\\ S_{\triangle ABC}&=&\frac 12 |AB||AC|\sin \theta,\\ S_{\triangle ABC}&=&\frac 12 |BC|h, \end{matrix}\right.\theta=\angle BAC$$
三式联立得 $h=\frac{\vec{AB}\times\vec{AC}}{|BC|}$。
因此可以用旋转卡壳来求凸多边形直径。
步骤
首先求出凸包,目的是把所有点按逆时针排序。然后枚举逆时针边,定义 $T$ 为当前的对踵点,若 $T$ 逆时针变动能增大到当前边的距离则改变 $T$,直到继续改变会导致距离减小为止。每次求出边(设为 $AB$)的对踵点 $T_i$ 后,分别用 $|AT_i|,|BT_i|$ 来更新答案,即凸多边形的直径。
时间复杂度 $O(n)$。
代码
db dis(vct a,vct b,vct x)//求出x到ab的距离
{
return fabs((a-x)*(b-x)/(a-b).dis());
}
int t=1;
db ans=0.0;
for(int i=1;i<tp;++i)
{
while(dis(h[i],h[i+1],h[t])<=dis(h[i],h[i+1],h[t+1]))
t=t%(tp-1)+1;
ans=std::max(ans,std::max((h[i]-h[t]).dis(),(h[i+1]-h[t]).dis()));//这里的dis是向量的模长
}
练习
UVA10173 Smallest Bounding Rectangle $O(n^2)$求最小覆盖矩形
洛谷 P3187 [HNOI2007] 最小矩形覆盖 $O(n\log n)$求最小覆盖矩形并输出矩形顶点(bzoj有spj)
半平面交
定义
半平面
一条直线和直线的一侧。半平面是一个点集,因此是一条直线和直线的一侧构成的点集。当包含直线时,称为闭半平面;当不包含直线时,称为开半平面。
解析式一般为 $Ax+By+C\ge 0$。
在计算几何中用向量表示,整个题统一以向量的左侧或右侧为半平面。

半平面交
半平面交是指多个半平面的交集。因为半平面是点集,所以点集的交集仍然是点集。在平面直角坐标系围成一个区域。
这就很像普通的线性规划问题了,得到的半平面交就是线性规划中的可行域。一般情况下半平面交是有限的,经常考察面积等问题的解决。
它可以理解为向量集中每一个向量的右侧的交,或者是下面方程组的解。
$$\left\{\begin{matrix}A_1x+B_1y+C\ge 0\\ A_2x+B_2y+C\ge 0\\ \cdots\end{matrix}\right.$$
多边形的核
如果一个点集中的点与多边形上任意一点的连线与多边形没有其他交点,那么这个点集被称为多边形的核。
把多边形的每条边看成是首尾相连的向量,那么这些向量在多边形内部方向的半平面交就是多边形的核。
解法 – S&I算法
极角排序
以前一直不会极角排序太丢人了甚至不会写Graham求凸包
C语言有一个库函数叫做atan2(double y,double x),可以返回 $\theta\in [-\pi,\pi]$(网上很多地方说左边是开的,不过对排序没有影响),$\theta =\arctan \frac{y}{x}$。
直接以向量为自变量,调用这个函数,以返回值为关键字排序,得到新的边(向量)集。
排序时,如果遇到共线向量(且方向相同),则取靠近可行域的一个。比如两个向量的极角相同,而我们要的是向量的左侧半平面,那么我们只需要保留左侧的向量。判断方法是取其中一个向量的起点或终点与另一个比较,检查是在左边还是在右边。
维护单调队列
因为半平面交是一个凸多边形,所以需要维护一个凸壳。因为后来加入的只可能会影响最开始加入的或最后加入的边(此时凸壳连通),只需要删除队首和队尾的元素,所以需要用单调队列。
我们遍历排好序了的向量,并维护另一个交点数组。当单队中元素超过2个时,他们之间就会产生交点。
对于当前向量,如果上一个交点在这条向量表示的半平面交的异侧,那么上一条边就没有意义了。
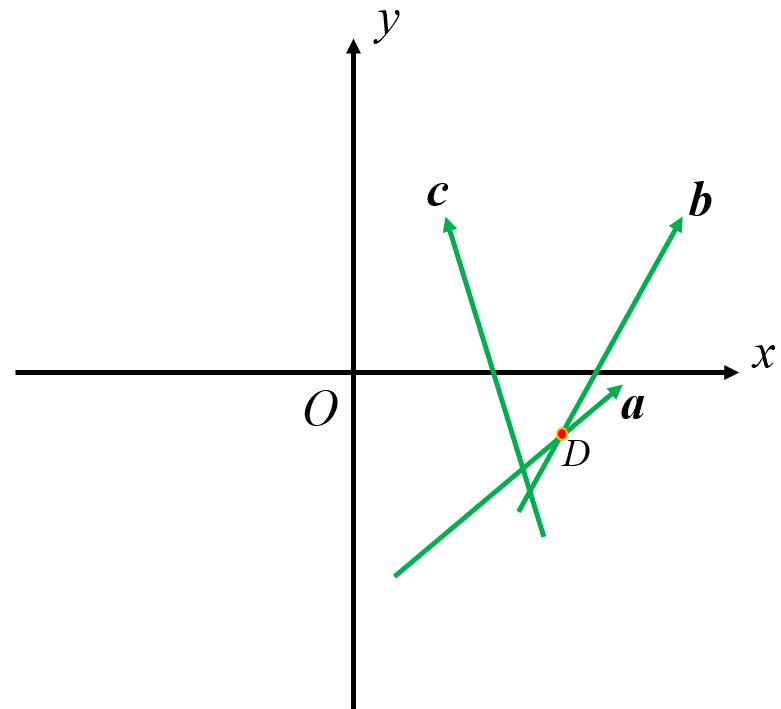
如上图,假设取向量左侧半平面。极角排序后,遍历顺序应该是 $\vec a\to\vec b\to\vec c$。当 $\vec a$ 和 $\vec b$ 入队时,在交点数组里会产生一个点 $D$(交点数组保存队列中相同下标的向量与前一向量的交点)。
接下来枚举到 $\vec c$ 时,发现 $D$ 在 $\vec c$ 的右侧。而因为产生 $D$ 的向量的极角一定比 $\vec c$ 要小,所以产生 $D$ 的向量(指 $\vec b$)就对半平面交没有影响了。
还有一种可能的情况是快结束的时候,新加入的向量会从队首开始造成影响。

仍然假设取向量左侧半平面。加入向量 $\vec f$ 之后,第一个交点 $G$ 就在 $\vec f$ 的右侧,我们把上面的判断标准逆过来看,就知道此时应该删除向量 $\vec a$,也即队首的向量。
最后用队首的向量排除一下队尾多余的向量。因为队首的向量会被后面的约束,而队尾的向量不会。此时它们围成了一个环,因此队首的向量就可以约束队尾的向量。
得到半平面交
如果半平面交是一个凸 $n$ 边形,最后在交点数组里会得到 $n$ 个点。我们再把它们首尾相连,就是一个统一方向(顺或逆时针)的 $n$ 多边形。
此时就可以用三角剖分求面积了。(求面积是最基础的考法)
偶尔会出现半平面交不存在或面积为0的情况,注意考虑边界。
时间复杂度 $O(n)$。
注意事项
upd on 2019.3.1
昨天晚上 @WG6101N 同学跟我说两个循环写反了会挂得很惨…稍微研究了一下原因。
当出现一个可以把队列里的点全部弹出去的向量(即所有队列里的点都在该向量的右侧),则我们必须先处理队尾,再处理队首。因此在循环中,我们先枚举
--r;的部分,再枚举++l;的部分,才不会错。原因如下。
一般情况下,我们在队列 (队列顺序为 $\left{\vec{u},\vec{v}\right}$) 后面加一条边(向量 $\vec w$),会产生一个交点 $N$ ,缩小 $\vec{v}$ 后面的范围。
但是毕竟每次操作都是一般的,因此可能会有把 $M$ 点“挤出去”的情况。
如果此时出现了向量 $\vec a$ ,使得 $M$ 在 $\vec a$ 的右侧,那么 $M$ 就要出队了。此时如果从队首枚举
++l,显然是扩大了范围。实际上 $M$ 点是由 $\vec u$ 和 $\vec v$ 共同构成的,因此需要考虑影响到现有进程的是 $\vec u$ 还是 $\vec v$。而因为我们在极角排序后,向量是逆时针顺序,所以 $\vec v$ 的影响要更大一些。就如上图,如果 $M$ 确认在 $\vec a$ 的右侧,那么此时 $\vec v$ 的影响一定不会对半平面交的答案作出任何贡献。
而我们排除队首的原因是当前向量的限制比队首向量要大,这个条件的前提是队列里有不止两个线段(向量),不然就会出现上面的情况。
所以一定要先排除队尾再排除队首。
代码
比较部分
friend bool operator <(seg x,seg y)
{
db t1=atan2((x.b-x.a).y,(x.b-x.a).x);
db t2=atan2((y.b-y.a).y,(y.b-y.a).x);//求极角
if(fabs(t1-t2)>eps)//如果极角不等
return t1<t2;
return (y.a-x.a)*(y.b-x.a)>eps;//判断向量x在y的哪边,令最靠左的排在最左边
}
增量部分
//pnt its(seg a,seg b)表示求线段a,b的交点
//s[]是极角排序后的向量
//q[]是向量队列
//t[i]是s[i-1]与s[i]的交点
//【码风】队列的范围是(l,r]
//求的是向量左侧的半平面
int l=0,r=0;
for(int i=1;i<=n;++i)
if((s[i]==s[i-1])==false)
{
//务必先检查队尾再检查队首
while(r-l>1&&(s[i].b-t[r])*(s[i].a-t[r])>eps)//如果上一个交点在向量右侧则弹出队尾
--r;
while(r-l>1&&(s[i].b-t[l+2])*(s[i].a-t[l+2])>eps)//如果第一个交点在向量右侧则弹出队首
++l;
q[++r]=s[i];
if(r-l>1)
t[r]=its(q[r],q[r-1]);//求新交点
}
while(r-l>1&&(q[l+1].b-t[r])*(q[l+1].a-t[r])>eps)//注意删除多余元素
--r;
t[r+1]=its(q[l+1],q[r]);//再求出新的交点
++r;
//这里不能在t里面++r需要注意一下……
练习
POJ 1279 Art Gallery 求多边形的核
虽然上面三个都是板子,但是需要注意的细节不同。
我的计算几何做题记录 可供参考






[…] wjyyy 《计算几何 学习笔记合集【凸包】【旋转卡壳】【半平面交】》 […]
向量叉乘那里是不是写错了啊…
“a×b的正负也可以理解为,把a顺时针方向转到b的方向,夹角为 θ。当 0≤θ<π 时值为正"
是逆时针吧?想了好久