bzoj 1597 [Usaco2008 Mar] 土地购买 题解【斜率优化】【DP】【贪心】
点击量:257
比较考思维的一道斜率优化。
Description
农夫 John 准备扩大他的农场,他正在考虑 $N (1\le N\le 50\ 000)$ 块长方形的土地。每块土地的长宽满足 $(1\le$ 宽 $\le 1\ 000\ 000, 1\le$ 长 $\le 1\ 000\ 000)$。每块土地的价格是它的面积,但 John 可以同时购买多块土地。 这些土地的价格是它们最大的长乘以它们最大的宽,但是土地的长宽不能交换。如果 John 买一块 $3\times 5$ 的地和一块 $5\times 3$ 的地,则他需要付 $5\times 5=25$。John 希望买下所有的土地,但是他发现分组来买这些土地可以节省经费。他需要你帮助他找到最小的经费。
Input
第 $1$ 行: 一个数:$N$。
第 $2..N+1$ 行: 第 $i+1$ 行包含两个数,分别为第 $i$ 块土地的长和宽。
Output
第一行: 最小的可行费用。
Sample Input
4 100 1 15 15 20 5 1 100Sample Output
500HINT
John 分 $3$ 组买这些土地:
第一组:$100\times 1$,
第二组:$1\times 100$,
第三组:$20\times 5$ 和 $15\times 15$。
每组的价格分别为 $100,100,300$, 总共 $500$。
题解:
我们先把所有的土地左下角对准 $(0,0)$,让下边和左边分别和 $x$ 轴、$y$ 轴对齐。然后得到右上角的坐标,即它们的长宽 $(a_i,b_i)$。
然后发现问题转化为了用若干左下角在原点的矩形覆盖所有点,矩形面积之和的最小值。
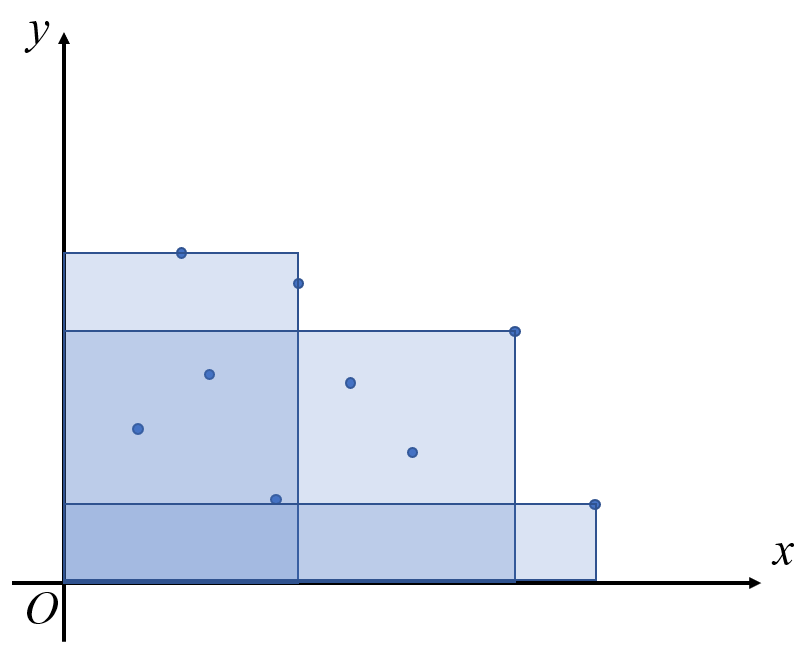
而随着矩形右边界的递增,上边界会逐渐减小。我们可以进行 dp。
先把所有的点/土地以横坐标/长为第一关键字,纵坐标/宽为第二关键字排序。令 $f[i]$ 表示买下前 $i$ 块土地的花费,则有方程
$$
f[i]=\min_{0\le j<i}\left\{f[j]+a_i\times\max_{j<k<i}\left\{b_k\right\}\right\}
$$
这样是 $O\left(n^2\right)$ 的。然而我们并没有什么优秀的类似前缀和的处理 $\max$ 的方法,此时重新考虑每个矩形的意义。
对于一个长宽分别为 $(A,B)$ 的矩形,它的意义为花费 $A\times B$ 的价格购买所有长不超过 $A$,宽不超过 $B$ 的土地。那么如果存在两个点 $(a_1,b_1),(a_2,b_2)$ 满足 $a_1\le a_2,b_1\le b_2$ ,则 $(a_1,b_1)$ 一定没有意义,遂删掉 $(a_1,b_1)$。
这样一来,整个点集合中也满足 $a_i\le a_{i+1},b_i\ge b_{i+1}$。和上面 dp 需要的过程一样。
这时我们发现,$\max_{j<k<i}\left\{b_k\right\}=b_{j+1}$。
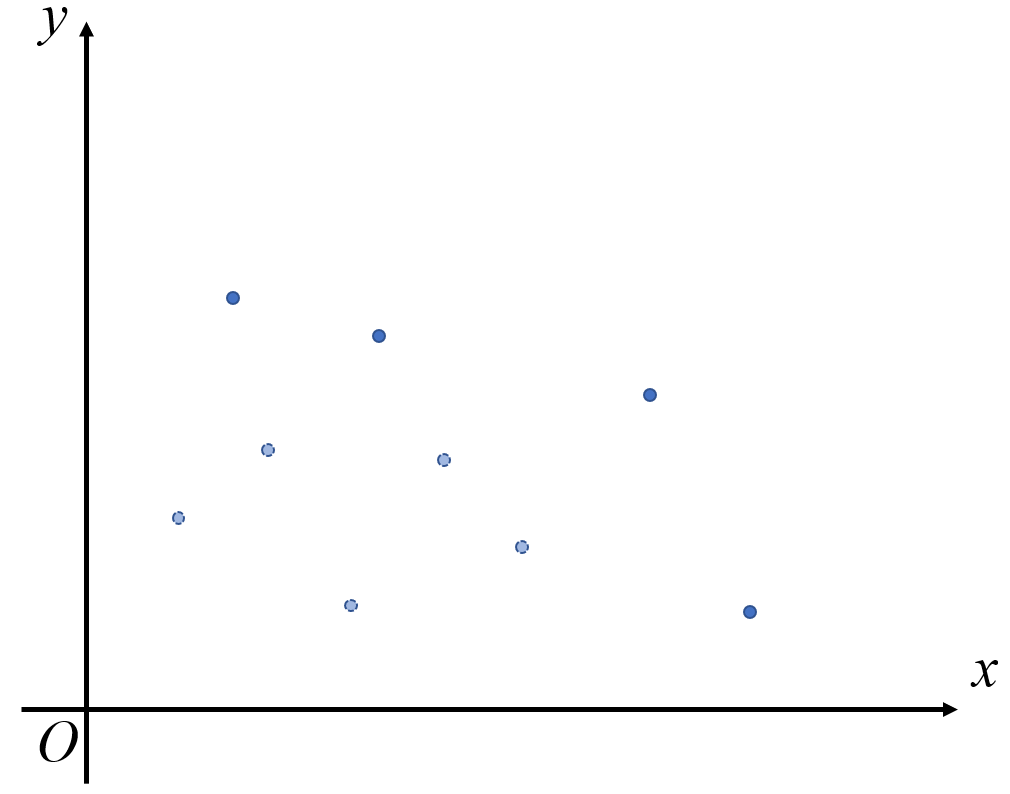
因此状态转移方程变成了
$$
f[i]=\min_{0\le j<i}\left\{f[j]+a_ib_{j+1}\right\}
$$
因此一定存在一个 $j$ 使得 $f[i]=f[j]+a_ib_{j+1}$。
此时对于一个确定的 $i$,$a_i$ 是常量。$f[j]$ 和 $b_{j+1}$ 是两个仅和 $j$ 有关的变量,$f[i]$ 是所求。
我们要使 $f[i]$ 最小,而 $a_ib_{j+1}$ 又是一个和 $i,j$ 同时有关的量,考虑斜率优化。
$$
f[i]=f[j]+a_ib_{j+1}\\
f[j]=-a_ib_{j+1}+f[i]\\
y=kx+b
$$
因此 $k=-a_i,\ b=f[i]$,此时有点集 $(x_j,y_j)$,分别对应 $b_{j+1},\ f[j]$。
又因为 $k$ 是递减的,所以我们维护了关于点集的上凸壳,然后单队斜率优化解决即可。
此时我们发现,当我们保留 $b_i$ 相等的相邻元素,会出现类似 $x_i=x_{i+1}$ 的情况,但是左侧那个是不会产生贡献的,因此左边可以不保留。$y_i$ 没有影响。
时间复杂度 $O(n)$。
Code:
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
struct plot
{
int a,b;
friend bool operator <(plot A,plot B)
{
if(A.a!=B.a)
return A.a<B.a;
return A.b<B.b;
}
}a[50050];
int q[50050],l=0,r=0;
ll f[50050],x[50050],y[50050],nxt[50050];
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;++i)
scanf("%d%d",&a[i].a,&a[i].b);
std::sort(a+1,a+1+n);
for(int i=n;i>=1;)
{
int t=i-1;
while(t&&a[t].b<=a[i].b)
--t;
nxt[t]=i;
i=t;
}
q[++r]=0;
x[0]=a[nxt[0]].b;
for(int i=nxt[0];i;i=nxt[i])
{
ll k=-a[i].a;
while(r-l>=2&&y[q[l+2]]-y[q[l+1]]<k*(x[q[l+2]]-x[q[l+1]]))
++l;
f[i]=y[q[l+1]]-k*x[q[l+1]];
x[i]=a[nxt[i]].b;
y[i]=f[i];
while(r-l>=2&&(y[i]-y[q[r]])*(x[q[r]]-x[q[r-1]])>(y[q[r]]-y[q[r-1]])*(x[i]-x[q[r]]))
--r;
q[++r]=i;
}
printf("%lld\n",f[n]);
return 0;
}


说点什么