洛谷 P1858 多人背包『第k优背包』 题解【DP】【背包】【归并】

点击量：219

   DP套归并！

目录

题目描述

求01背包前k优解的价值和，且背包必须装满。

输入输出格式

输入格式：

第一行三个数\(K,V,N\)

接下来每行两个数，表示体积和价值

输出格式：

前\(k\)优解的价值和

输入输出样例

输入样例#1：

2 10 5
3 12
7 20
2 4
5 6
1 1

输出样例#1：

57

说明

对于\(100\%\)的数据,\(K\le 50,V\le 5000,N\le 200\)

题解：

   因为第\(k\)优解与第\(k+1\)优解没有严格与某个物品的选或不选有关系，因此不能用分层图转移的思想来做。不过因为最优解到第k优解的答案总是（非严格）递增的，所以考虑排序取最优，那么对哪些数据排序呢？

   对于这个题的状态，设为f[i][j]，表示已经装\(i\)空间的物品的第\(j\)优解（压掉了第一维）。对于一般的背包，状态转移方程为

f[i][j]=第j大(f[i][k1],f[i-c][k2]);

   其中\(k1-1+k2-1=j-1\)，因为前\(k1-1\)个数和前\(k2-1\)个数凑成了\(f[i]\)的前\(j-i\)优解，就是归并的思想。假设第一个队列为\(f[i][]\),第二个队列为\(f[i-c][]+v\)，我们每次取最优的那个，当\(f[i][1]\)弹出后，就用\(f[i][2]\)和\(f[i-c][1]\)比，类似归并把答案存在另一个数组中（防止冲突），最后再\(\tt copy\)回\(f[i]\)的前\(k\)优解。

我们有两个单增序列，要求它们的前k大值

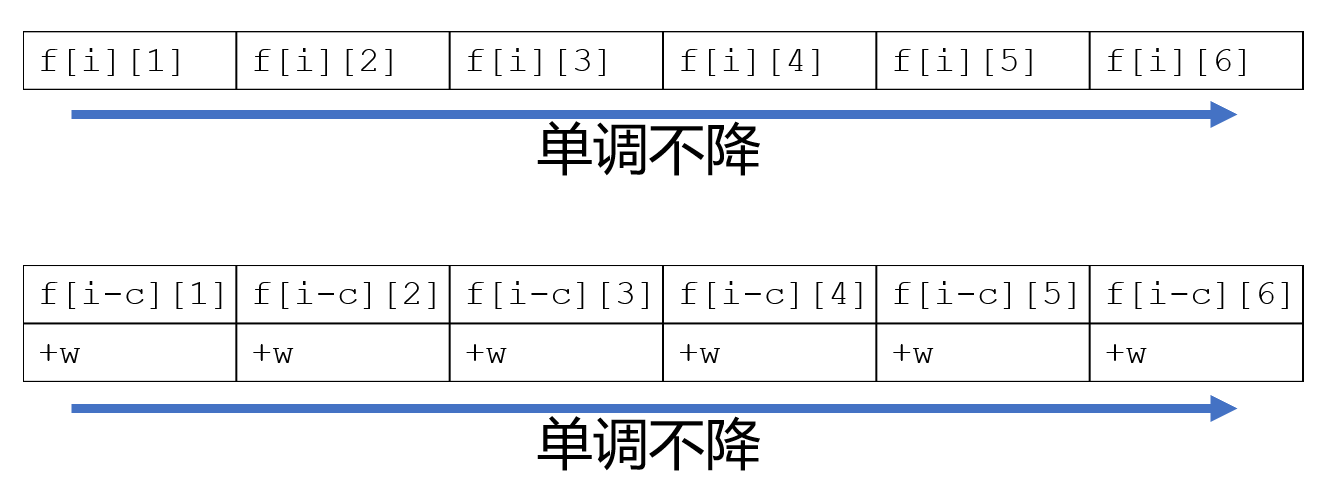
可以用归并的思路，用两个头指针判断哪个更大，就把哪个放到临时队列里。

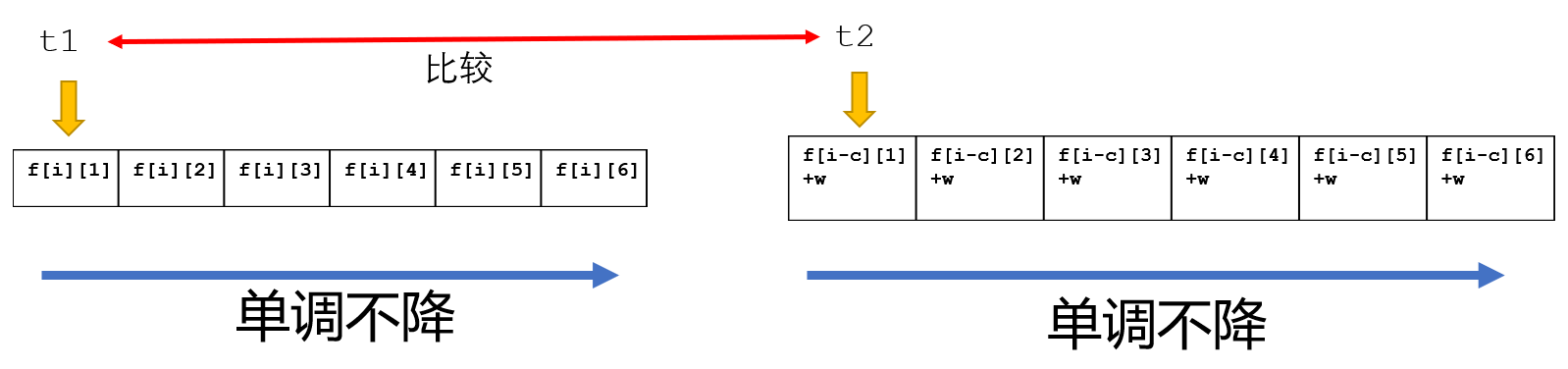
最后把临时队列再赋值给\(f[i][1…k]\)就可以了。

   非常正常容易想到的简单的归并思路题///。

Code：

#include<cstdio>
#include<cstring>
int max(int x,int y)
{
    return x>y?x:y;
}
int f[5010][55];
int tmp[55];
int main()
{
    memset(f,-0x3f,sizeof(f));
    f[0][1]=0;
    int k,n,v,c,w;
    scanf("%d%d%d",&k,&v,&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&c,&w);
        for(int j=v;j>=c;j--)
        {
            int t1=1,t2=1;//归并用
            for(int l=1;l<=k;l++)
                if(f[j][t1]<f[j-c][t2]+w)
                    tmp[l]=f[j-c][t2++]+w;
                else
                    tmp[l]=f[j][t1++];
            for(int l=1;l<=k;l++)
                f[j][l]=tmp[l];
        }
    }
    int ans=0;
    for(int i=1;i<=k;i++)
        ans+=f[v][i];
    printf("%d\n",ans);
    return 0;
}