洛谷 P2473 [SCOI2008]奖励关 题解【DP】【状态压缩】【概率期望】

点击量：126

   第一次遇到概率/期望DP，收获挺多。

目录

题目描述

你正在玩你最喜欢的电子游戏，并且刚刚进入一个奖励关。在这个奖励关里，系统将依次随机抛出k次宝物，每次你都可以选择吃或者不吃（必须在抛出下一个宝物之前做出选择，且现在决定不吃的宝物以后也不能再吃）。

 

宝物一共有n种，系统每次抛出这n种宝物的概率都相同且相互独立。也就是说，即使前k-1次系统都抛出宝物1（这种情况是有可能出现的，尽管概率非常小），第k次抛出各个宝物的概率依然均为1/n。

 

获取第 i 种宝物将得到Pi分，但并不是每种宝物都是可以随意获取的。第i种宝物有一个前提宝物集合Si。只有当Si中所有宝物都至少吃过一次，才能吃第i 种宝物（如果系统抛出了一个目前不能吃的宝物，相当于白白的损失了一次机会）。注意，Pi 可以是负数，但如果它是很多高分宝物的前提，损失短期利益而吃掉这个负分宝物将获得更大的长期利益。

 

假设你采取最优策略，平均情况你一共能在奖励关得到多少分值？

 

输入输出格式

输入格式：

第一行为两个正整数k 和n，即宝物的数量和种类。以下n行分别描述一种宝物，其中第一个整数代表分值，随后的整数依次代表该宝物的各个前提宝物（各宝物编号为1到n），以0结尾。

 

输出格式：

输出一个实数，保留六位小数，即在最优策略下平均情况的得分。

 

输入输出样例

输入样例#1：

1 2

1 0

2 0

输出样例#1：

1.500000

输入样例#2：

6 6

12 2 3 4 5 0

15 5 0

-2 2 4 5 0

-11 2 5 0

5 0

1 2 4 5 0

输出样例#2：

10.023470

说明

1 <= k <= 100, 1 <= n <= 15，分值为[-106,106]内的整数。

 

解法：

   题目让求一个平均值，并且类似期望，因此我们要求按每种顺序出现宝物的最大期望值。如何控制期望就是一个难题。

   如果我们试着模拟这个过程，先看N≤16的范围，就会想到状态压缩，这样我们就可以在O(1)的时间内判断转移是否合法。当合法时转移状态，不合法时不吃。但是这时问题来了，不合法时如果不吃算一个状态，那么错过了某个宝箱实际上又是一个状态是不合题意的。如果算两个状态，那么期望是按多大的概率来算呢？

   有些过程可以模拟为以下这样

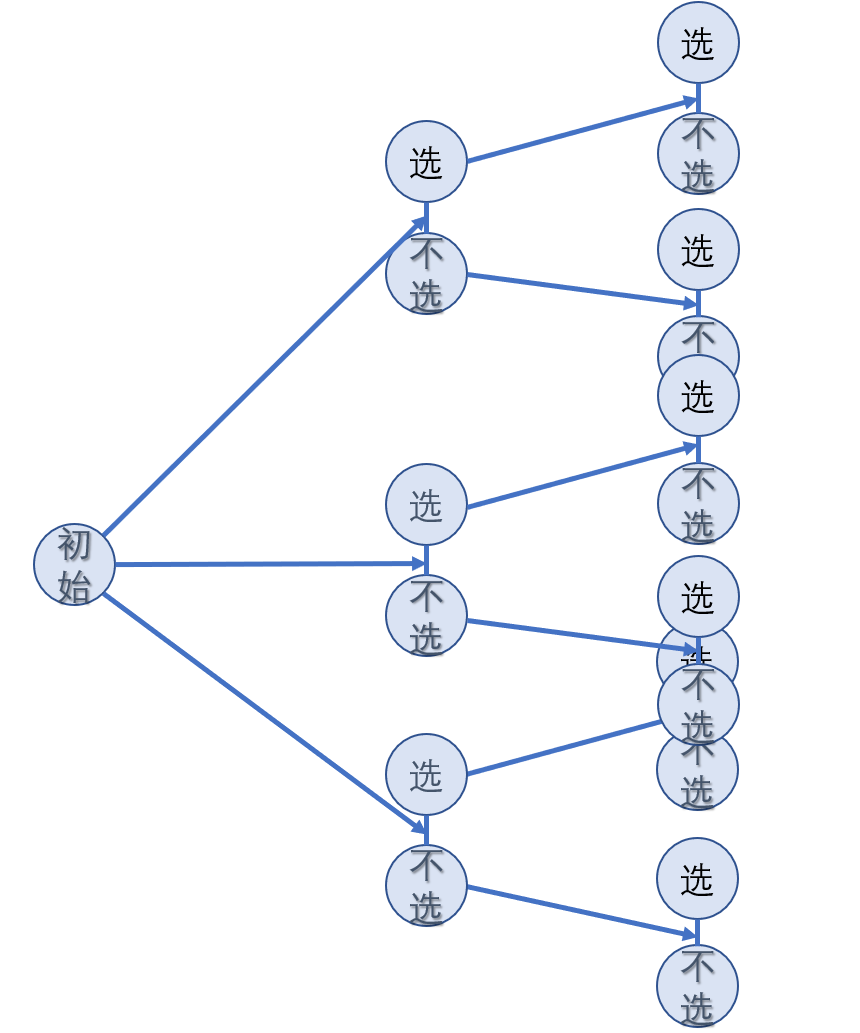(省略了第二层的一些状态，出度应为3)

   这样看来，每一步的状态只需要判断是否合法，再转移，总的状态还是$ n\times 2^m$。但是合法不合法也是有冲突的，因为我们要控制最大期望，也是我们决策的主导方向，所以有时不选会比选更优。这时前面的选或不选概率就会发生改变，像这样

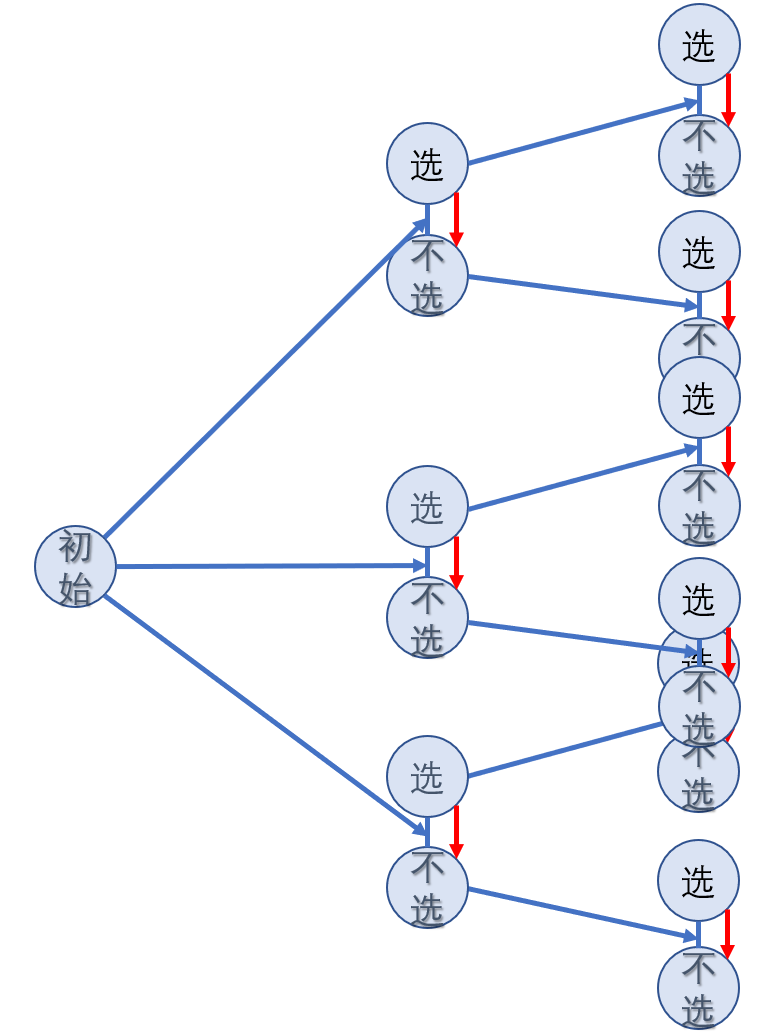(同上省略了第二层的一些状态，出度应为3)

   那么当选和不选对最大期望有影响时，概率也会改变。

   我们不妨换个思路，因为宝物掉下来的概率仍然平均，所以我们选或不选对宝物的掉落没有丝毫影响。我们为了无后效性，试着从最终状态往前转移。f[i][j]表示接到第i个宝物前，状态为j，此时离最终状态的最大期望是多少。倒着转移有一个好处，就是可以知道哪里可以合法地被转移，有多少种转移方式。在这里只需要枚举1到n这些物品是否合法，也就是它们的前提物品有没有全部被选，如果不合法，就不能加上这个物品的得分；如果合法，判断这个物品选或不选对答案的影响（因为物品会有负数得分），转移前一层选或不选指向的状态，再累计期望值。

   看到上面的树形图，我们知道，尽管第i次掉落k号物品的概率仍然是$ \frac 1n$，但是它会由前面的$ \frac 1{n^{i-1}}$个状态叠加过来，所以这时每层的期望会缩小n倍。因此我们倒着做，当一个状态在被转移走之前，除上n，那么做到最开始一层后，第i层的期望就被除了$ n^i$次。这时最初的状态f[1][0]就是答案了。

   这就是期望DP的一般做法：从后往前推，从合法状态累加后转移，不合法状态直接转移，按题目要求转移最大或最小值。最终状态为初始没有选的状态，输出答案。

Code：

#include<cstdio>
#include<cstring>
double max(double x,double y)
{
    return x>y?x:y;
}
double f[120][33333];
int scor[20],d[20];
int main()
{
    memset(d,0,sizeof(d));
    int m,n,u;
    scanf("%d%d",&m,&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&scor[i]);
        scanf("%d",&u);
        while(u!=0)
        {
            d[i]|=(1<<(u-1));//状态压缩前提物品
            scanf("%d",&u);
        }
    }
    for(int i=m;i>=1;i--)
        for(int j=0;j<1<<n;j++)
        {
            f[i][j]=0;
            for(int k=1;k<=n;k++)//取出哪一位
            {
                if((j&d[k])==d[k])//合法取最大
                    f[i][j]+=max(f[i+1][j],f[i+1][j|(1<<(k-1))]+scor[k]);
                else//不合法必须转移
                    f[i][j]+=f[i+1][j];
            }
            f[i][j]/=n;//每层结束时除n表示当前到这里的概率为1/n
        }
    printf("%.6lf\n",f[1][0]);
    return 0;
}