洛谷 P1436 棋盘分割 题解【搜索】/【区间DP】【前缀和】

点击量：169

   为什么正解是DP。。。

目录

题目描述

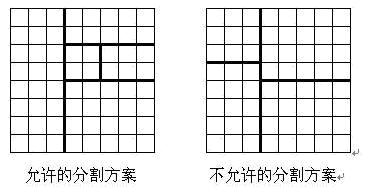
将一个８×８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的两部分中的任意一块继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的平方和最小。

请编程对给出的棋盘及n，求出平方和的最小值。

输入输出格式

输入格式：

第1行为一个整数n(1<n<15)。

 

第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

 

输出格式：

仅一个数，为平方和。

 

输入输出样例

输入样例#1：

3

1 1 1 1 1 1 1 3

1 1 1 1 1 1 1 1

1 1 1 1 1 1 1 1

1 1 1 1 1 1 1 1

1 1 1 1 1 1 1 1

1 1 1 1 1 1 1 1

1 1 1 1 1 1 1 0

1 1 1 1 1 1 0 3

输出样例#1：

1460

题解：

   题目一看上去：两边只选一边分，二叉树？但是可以沿着任何一条边分，状态太多不好处理。于是试着搜索，权值和用二维前缀和优化。

   因为棋盘固定为8×8，所以对于初始状态，枚举1~7行（作为上半边最下一行），再枚举分上半边还是下半边，如果选择一半，就计算另一半权值和的平方，加入sum，dfs另一半。还要枚举1~7列，dfs枚举左半边和右半边。

   由此可以推到一般情况，dfs带入左上角坐标$ (lx,ly)$、右下角坐标$ (rx,ry)$确定一个矩形。枚举$ [lx,ry)$行，与上面做相同的操作，各计算两边的权值和平方（一边dfs出来后算另一边时记得减掉），另一边带入dfs。

   当dfs进行到第n次时，就终止过程（要在函数开始时判断，不能执行第n次）。此时计算当前矩形权值和的平方，加入sum，与答案进行比较取较小值。

剪枝：

    最优解剪枝：这个搜索只用这一个剪枝就可以把代码从50分优化到100分，当目前sum大于已经计算出来的minn时，直接返回。

DP版题解：

   看作一个区间DP，因为这种分割形式类似一维，所以像区间DP一样枚举断点。每一层（被切割了i次）状态由i-1转移，枚举横切纵切，并取最小值。除第0层外，初始化为inf。

Code dfs：

#include<cstdio>
#include<cstring>
int min(int x,int y)
{
    return x<y?x:y;
}
int b[10][10];
int minn=0x3fffffff;
int cal(int lx,int ly,int rx,int ry)//计算前缀和
{
    return b[rx][ry]-b[lx-1][ry]-b[rx][ly-1]+b[lx-1][ly-1];
}
int sum=0,n;
void dfs(int k,int lx,int ly,int rx,int ry)
{
    if(sum>minn)
        return;
    if(k+1==n)
    {
        int now=cal(lx,ly,rx,ry);
        now*=now;//最后加上这一矩阵的平方
        minn=min(sum+now,minn);
        return;
    }
    //枚举从第i行切
    for(int i=lx;i<rx;i++)
    {
        int half=cal(i+1,ly,rx,ry)*cal(i+1,ly,rx,ry);
        sum+=half;
        dfs(k+1,lx,ly,i,ry);
        sum-=half;
        half=cal(lx,ly,i,ry)*cal(lx,ly,i,ry);
        sum+=half;
        dfs(k+1,i+1,ly,rx,ry);
        sum-=half;
    }
    //枚举从第i列切
    for(int i=ly;i<ry;i++)
    {
        int half=cal(lx,i+1,rx,ry)*cal(lx,i+1,rx,ry);
        sum+=half;
        dfs(k+1,lx,ly,rx,i);
        sum-=half;
        half=cal(lx,ly,rx,i)*cal(lx,ly,rx,i);
        sum+=half;
        dfs(k+1,lx,i+1,rx,ry);
        sum-=half;
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=8;i++)
        for(int j=1;j<=8;j++)
        {
            scanf("%d",&b[i][j]);
            b[i][j]+=b[i-1][j]+b[i][j-1];
            b[i][j]-=b[i-1][j-1];
        }
    sum=0;
    dfs(0,1,1,8,8);//初态
    printf("%d\n",minn);
    return 0;
}

Code DP：

#include<cstdio>
#include<cstring>

int f[18][9][9][9][9];
int b[9][9];
int min(int x,int y)
{
    return x<y?x:y;
}
int cal(int lx,int ly,int rx,int ry)
{
    return b[rx][ry]-b[lx-1][ry]-b[rx][ly-1]+b[lx-1][ly-1];
}
int main()
{
    memset(f,0x3f,sizeof(f));
    int n;
    scanf("%d",&n);
    for(int i=1;i<=8;i++)
        for(int j=1;j<=8;j++)
        {
            scanf("%d",&b[i][j]);
            b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
        }
    for(int lx=1;lx<=8;lx++)//初始化
        for(int ly=1;ly<=8;ly++)
            for(int rx=lx;rx<=8;rx++)
                for(int ry=ly;ry<=8;ry++)
                    f[0][lx][ly][rx][ry]=cal(lx,ly,rx,ry)*cal(lx,ly,rx,ry);

    for(int k=1;k<n;k++)
        for(int lx=1;lx<=8;lx++)
            for(int ly=1;ly<=8;ly++)
                for(int rx=lx;rx<=8;rx++)
                    for(int ry=ly;ry<=8;ry++)
                    {
                        for(int i=lx;i<rx;i++)
                            f[k][lx][ly][rx][ry]=min(f[k][lx][ly][rx][ry],min(f[k-1][lx][ly][i][ry]+cal(i+1,ly,rx,ry)*cal(i+1,ly,rx,ry),f[k-1][i+1][ly][rx][ry]+cal(lx,ly,i,ry)*cal(lx,ly,i,ry)));
                        for(int i=ly;i<ry;i++)
                            f[k][lx][ly][rx][ry]=min(f[k][lx][ly][rx][ry],min(f[k-1][lx][ly][rx][i]+cal(lx,i+1,rx,ry)*cal(lx,i+1,rx,ry),f[k-1][lx][i+1][rx][ry]+cal(lx,ly,rx,i)*cal(lx,ly,rx,i)));
                    }
    printf("%d\n",f[n-1][1][1][8][8]);
    return 0;
}