洛谷 P5339 [TJOI2019]唱、跳、rap和篮球 题解【容斥】【meet-in-middle】【递推】【排列组合】
点击量:499
计数问题首推容斥,然后再解决一些棘手的组合问题?
题目描述
大中锋的学院要组织学生参观博物馆,要求学生们在博物馆中排成一队进行参观。
他的同学可以分为四类:一部分最喜欢唱、一部分最喜欢跳、一部分最喜欢 rap,还有一部分最喜欢篮球。
如果队列中 $k,k + 1,k + 2,k + 3$ 位置上的同学依次,最喜欢唱、最喜欢跳、最喜欢 rap、最喜欢篮球,那么他们就会聚在一起讨论蔡徐坤。
大中锋不希望这种事情发生,因为这会使得队伍显得很乱。
大中锋想知道有多少种排队的方法,不会有学生聚在一起讨论蔡徐坤。
两个学生队伍被认为是不同的,当且仅当两个队伍中至少有一个位置上的学生的喜好不同。
由于合法的队伍可能会有很多种,种类数对 $998244353$ 取模。
输入格式
输入数据只有一行。
每行 $5$ 个整数,第一个整数 $n$,代表大中锋的学院要组织多少人去参观博物馆。
接下来四个整数 $a、b、c、d$,分别代表学生中最喜欢唱的人数、最喜欢跳的人数、最喜欢 rap 的人数和最喜欢篮球的人数。
保证 $a + b + c + d ≥ n$。
输出格式
每组数据输出一个整数,代表你可以安排出多少种不同的学生队伍,使得队伍中没有学生聚在一起讨论蔡徐坤。结果对 $998244353$ 取模。
样例 1 输入
4 4 3 2 1样例 1 输出
174样例 2 输入
996 208 221 132 442样例 2 输出
442572391数据范围与约定
对于 $20\%$ 的数据,有 $n = a = b = c = d ≤ 500$;
对于 $100\%$ 的数据,有 $n ≤ 1000,a,b,c,d ≤ 500$。
题解
$\newcommand{\C}{\mathrm{C}}$事实上洛谷上有很多直接推式子 NTT 和生成函数的题解。
不过没学过生成函数,暴力容斥了。
感觉这种在序列上的组合问题会一下子想到容斥。
用 c,t,r,l 分别表示喜欢唱、跳、rap、篮球的同学。
首先,如果要用容斥解决的话,可以从序列中连续的 c,t,r,l 的个数入手。
首先需要计算当 $a,b,c,d$ 都无穷大,即每个位置都可以放 c,t,r,l 中任意一个同学时,长为 $n$ 的序列中有 $m$ 个连续的 c,t,r,l 的方案。
定义 $\C_n^m$ 为长为 $n$ 的序列里选 $m$ 个元素,且被选出的任意两个元素之间距离不小于 $4$,那么上面所提到的方案的计算式就是 $\C_{n-3}^m$。
而根据组合意义,$\C_n^m=\sum_{i=0}^{n-3}\C_{i}^{m-1}$。
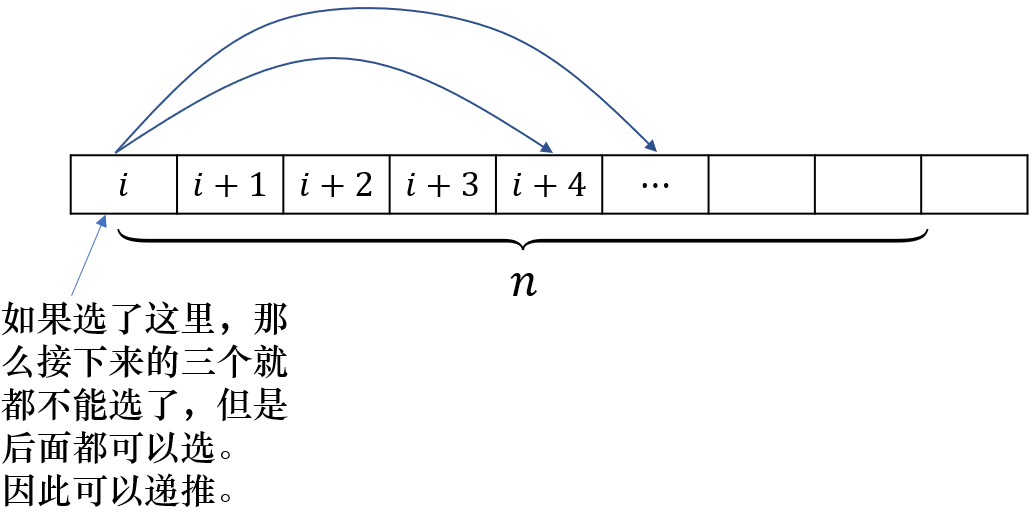
而在本题中,$n\le 1000$,因此有效的 $\C_n^m$ 不超过 $1000^2$ 个,而且 $0\le m\le\lfloor\frac{n-1}4\rfloor+1$,所以常数也比较小。
递推时,只需要处理 $\C_i^m$ 关于 $i$ 的前缀和 $\C_0^m+\C_1^m+\cdots$,就可以做到 $O(n^2)$ 了。
有了所有的 $\C_n^m$ 之后,就可以开始容斥了。
当序列中有至少 $0$ 个连续的 c,t,r,l 时,所有位置上都可以任选。
这是一个可重组合数问题,但是由于只有四种元素,我们可以先确定四种喜好的同学分别有多少个。四种喜好的人数依次设为 $A,B,C,D(0\le A\le a,0\le B\le b,0\le C\le c,0\le D\le d)$,令 $k=\min\{a,b,c,d\}$。
那么接下来就是求合法的($A+B+C+D=n$)四元组 $(A,B,C,D)$ 的个数了。
直接枚举是 $O(k^3)$ 的,而对于每个 $i(0\le i\le\lfloor\frac{n-1}4\rfloor)$ 都要做一遍,这是承受不了的。
我们可以通过枚举二元组 $(A,B)$ 来预处理有多少个二元组满足 $A+B=t$,再枚举 $(C,D)$,和 $(C,D)$ 能匹配上的 $(A,B)$ 的数量就是满足 $A+B=n-C-D$ 的二元组 $(A,B)$ 数量。
也就是说,如果用 $cnt_t$ 来表示有多少个二元组 $(A,B)$ 满足 $A+B=t$,那么对于二元组 $(C,D)$,能匹配上它的有 $cnt_{n-C-D}$ 种。
上面解释了一个 meet-in-middle 的思路,复杂度为 $O(k^2)$,小常数 $O(nk^2)$ 级别还是可以接受的。
这时,我们得到了合法的四元组 $(A,B,C,D)$ 的数目了,现在转化为可重排列问题,这个用阶乘算一下就可以了。
但是我们只知道数目,不知道具体的 $(A,B,C,D)$。可重排列数中,分子上是 $n!$,而分母上是 $A!B!C!D!$。根据不同的 $(A,B,C,D)$,这个数不尽相同。
我们可以在上面算贡献的时候,对于二元组 $(A,B)$,对 $cnt_{A+B}$ 的贡献就是 $\frac{1}{A!B!}$;而当 $(C,D)$ 找回去的时候,就用 $\frac1{C!D!}$ 去乘 $cnt_{n-C-D}$。
这样就有了“至少 $0$ 个”,也就是任意位置上都随便放的方案数。
至少 $1$ 个的方案数,就是把上面“至少 $0$ 个”方案数中的 $n$ 换成 $n-4$,然后乘上上面所定义的 $\C_n^1$。
依此类推,直到至少 $k$ 个会把 c,t,r,l 中最少的一个用完,或者至少 $\frac n4$ 个。连续的 c,t,r,l 填满了所有位置。
答案就是至少 $0$ 个 $-$ 至少 $1$ 个 $+$ 至少 $2$ 个 $+\cdots+(-1)^{\min(k,\frac n4)}\times$ 至少 $\min(k,\frac n4)$ 个。
时间复杂度 $O(nk^2)$,常数在 $\frac 14$ 左右。
trick:
从这题可以看出来组合数的一种推法。当间隔不大于 $1$ 时,也就是原意义下的组合数,$\C_n^m=\sum_{i=0}^{n-1}\C_i^{m-1}$。
Code:
#include<cstdio>
#include<cstring>
#define p 998244353
#define ll long long
int Min(int x,int y){return x<y?x:y;}
ll qpow(ll x,ll y)
{
ll ans=1;
while(y)
{
if(y&1)
ans=ans*x%p;
x=x*x%p;
y>>=1;
}
return ans;
}
int f[1010][300];
ll sum[300],func[1010],inv[1010];
int cnt[1010];
int main()
{
int n;
scanf("%d",&n);
func[0]=1;
f[0][0]=1;
for(int i=1;i<=n;++i)
{
func[i]=func[i-1]*i%p;
f[i][0]=1;
for(int j=1;j<=i/4;++j)
{
sum[j-1]=(sum[j-1]+f[i-4][j-1])%p;
f[i][j]=sum[j-1];
}
}
inv[n]=qpow(func[n],p-2);
for(int i=n-1;i>=0;--i)
inv[i]=inv[i+1]*(i+1)%p;
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
int mn=a<b?(a<c?(a<d?a:d):(c<d?c:d)):(b<c?(b<d?b:d):(c<d?c:d)),ans=0;
//int mn=Min(Min(a,b),Min(c,d)),ans=0;
for(int i=0,tot=n;i<=mn&&i<=n/4;++i,--a,--b,--c,--d,tot-=4)
{
memset(cnt,0,sizeof(cnt));
long long op=0;
for(int A=0;A<=a;++A)
for(int B=0;B<=b;++B)
cnt[A+B]=(cnt[A+B]+inv[A]*inv[B])%p;
for(int C=0;C<=c;++C)
for(int D=0;D<=d&&C+D<=tot;++D)
op=(op+cnt[tot-C-D]*inv[C]%p*inv[D])%p;
op=op*func[tot]%p;
if(i&1)
ans=(ans+p-op*f[n][i]%p)%p;
else
ans=(ans+op*f[n][i]%p)%p;
}
printf("%d\n",ans);
return 0;
}


说点什么