CF1336A Linova and Kindom 【图论】【树形DP】【贪心】

点击量：448

一道比较简单的树题，如果题目想复杂了可以找一些性质简化一下。

目录

Description

Writing light novels is the most important thing in Linova’s life. Last night, Linova dreamed about a fantastic kingdom. She began to write a light novel for the kingdom as soon as she woke up, and of course, she is the queen of it.

There are $n$ cities and $n-1$ two-way roads connecting pairs of cities in the kingdom. From any city, you can reach any other city by walking through some roads. The cities are numbered from $1$ to $n$, and the city $1$ is the capital of the kingdom. So, the kingdom has a tree structure.

As the queen, Linova plans to choose exactly $k$ cities developing industry, while the other cities will develop tourism. The capital also can be either industrial or tourism city.

A meeting is held in the capital once a year. To attend the meeting, each industry city sends an envoy. All envoys will follow the shortest path from the departure city to the capital (which is unique).

Traveling in tourism cities is pleasant. For each envoy, his happiness is equal to the number of tourism cities on his path.

In order to be a queen loved by people, Linova wants to choose $k$ cities which can maximize the sum of happinesses of all envoys. Can you calculate the maximum sum for her?

Input

The first line contains two integers $n$ and $k$ $(2\le n\le 2\cdot 10^5, 1\le k<n)$ — the number of cities and industry cities respectively.

Each of the next $n-1$ lines contains two integers $u$ and $v (1\le u,v\le n)$, denoting there is a road connecting city $u$ and city $v$.

It is guaranteed that from any city, you can reach any other city by the roads.

Output

Print the only line containing a single integer — the maximum possible sum of happinesses of all envoys.

Examples

input

7 4
1 2
1 3
1 4
3 5
3 6
4 7

output

7

input

4 1
1 2
1 3
2 4

output

2

input

8 5
7 5
1 7
6 1
3 7
8 3
2 1
4 5

output

9

Note

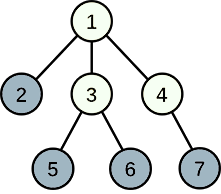
In the first example, Linova can choose cities $2,5,6,7$ to develop industry, then the happiness of the envoy from city $2$ is $1$, the happiness of envoys from cities $5, 6, 7$ is $2$. The sum of happinesses is $7$, and it can be proved to be the maximum one.

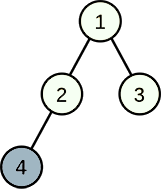
In the second example, choosing cities $3, 4$ developing industry can reach a sum of $3$, but remember that Linova plans to choose exactly $k$ cities developing industry, then the maximum sum is $2$.

题意：

给出一个国家的地图，是一棵树，每个节点是一个城市，首都为 $1$ 号点，每个城市是旅游城市或工业城市。工业城市的人需要通过最短的道路到首都开会，这个人的幸福指数是他经过的旅游城市的数量。现在选择 $k$ 个城市作为工业城市，求最大的总幸福度。

题解：

读懂题意后可以很快地发现一个树剖的贪心，因为每个点的 happiness 可以很容易地处理掉。

我们树剖建一棵最大值线段树，每个点的初始值为深度。每次找最大值选出来，然后把它的所有祖先权值都 $-1$，这样操作 $k$ 次，复杂度是 $k\log^2n$ 的。

这个题的正确做法是一个简单的树形 DP+贪心。

我们上来要选的点一定是最深的那些点，选完它们之后，根据树剖做法的分析，它们的祖先就会有更少的贡献。

而考虑贪心，如果一个点 $x$ 被选，那么它的子树一定都被选完了。而子树选完后，它的贡献值就减少了 $sz[x]-1$。所以每个点的最终贡献值是可以计算出来的，为 $d[x]-sz[x]+1$。

这样的话，一遍 DFS 就搞定了。

因为要取前 $k$ 大贡献，所以需要排序。总时间复杂度为 $O(n\log n)$。

Code：

#include<cstdio>
#include<cstring>
#include<algorithm>
struct edge
{
    int n,nxt;
    edge(int n,int nxt)
    {
        this->n=n;
        this->nxt=nxt;
    }
    edge(){}
}e[400000];
int ecnt=-1,head[200100];
void add(int from,int to)
{
    e[++ecnt]=edge(to,head[from]);
    head[from]=ecnt;
    e[++ecnt]=edge(from,head[to]);
    head[to]=ecnt;
}
int sz[200100],d[200100];
void dfs(int x,int from)
{
    sz[x]=1;
    for(int i=head[x];~i;i=e[i].nxt)
        if(e[i].n!=from)
        {
            d[e[i].n]=d[x]+1;
            dfs(e[i].n,x);
            sz[x]+=sz[e[i].n];
        }
    d[x]-=sz[x]-1;
}
int main()
{
    memset(head,-1,sizeof(head));
    int n,k,u,v;
    long long tot=0;
    scanf("%d%d",&n,&k);
    for(int i=1;i<n;++i)
    {
        scanf("%d%d",&u,&v);
        add(u,v);
    }
    dfs(1,1);
    std::sort(d+1,d+1+n);
    for(int i=n;i>n-k;--i)
        tot+=d[i];
    printf("%lld\n",tot);
    return 0;
}