洛谷 P1158 NOIP2010普及组 导弹拦截 题解【枚举】【前缀最大值】【快速排序】

点击量：148

   我估计CCF也经历了11年的韬光养晦。。。

目录

题目描述

经过11年的韬光养晦，某国研发出了一种新的导弹拦截系统，凡是与它的距离不超过其工作半径的导弹都能够被它成功拦截。当工作半径为0时，则能够拦截与它位置恰好相同的导弹。但该导弹拦截系统也存在这样的缺陷：每套系统每天只能设定一次工作半径。而当天的使用代价，就是所有系统工作半径的平方和。

 

某天，雷达捕捉到敌国的导弹来袭。由于该系统尚处于试验阶段，所以只有两套系统投入工作。如果现在的要求是拦截所有的导弹，请计算这一天的最小使用代价。

 

输入输出格式

输入格式：

第一行包含4个整数$ x_1$、$ y_1$、$ x_2$、$ y_2$ ，每两个整数之间用一个空格隔开，表示这两套导弹拦截系统的坐标分别为$ (x_1,y_1)$、$ (x_2,y_2)$ 。 第二行包含1个整数N，表示有N颗导弹。接下来N行，每行两个整数 x,y，中间用 一个空格隔开，表示一颗导弹的坐标(x,y)。不同导弹的坐标可能相同。

 

输出格式：

一个整数，即当天的最小使用代价。

 

输入输出样例

输入样例#1：

0 0 10 0

2

-3 3

10 0

输出样例#1：

18

输入样例#2：

0 0 6 0

5

-4 -2

-2 3

4 0

6 -2

9 1

输出样例#2：

30

说明

两个点$ (x_1,y_1)$、$ (x_2,y_2)$ 之间距离的平方是$ (x_1-x_2)^2+(y_1-y_2)^2$ 。

两套系统工作半径$ r_1,r_2$的平方和，是指$ r_1,r_2$分别取平方后再求和，即$ r_1^2+r_2^2$。

【样例1说明】

样例1中要拦截所有导弹，在满足最小使用代价的前提下，两套系统工作半径的平方分别为

$18$

18 和

$0$

0 。

【样例2说明】

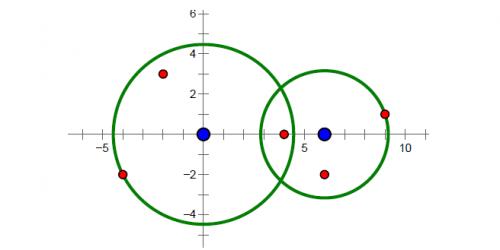
样例2中的导弹拦截系统和导弹所在的位置如下图所示。要拦截所有导弹，在满足最小使用代价的前提下，两套系统工作半径的平方分别为20和10。

【数据范围】

对于10%的数据，N=1

对于20%的数据，1<=N<=2

对于40%的数据，1<=N<=100

对于70%的数据，1<=N<=1000

对于100%的数据，1<=N<=100000，且所有坐标分量的绝对值都不超过1000。

   一眼看上去好像是个贪心，于是……70pnts？？

   贪心思路：如果一个点离1号近，它就投靠1号，否则投靠2号，计算出1号和2号所有投靠中和最大的方案。

    我们举个例子，如果很多很多点都在1号附近，而只有一个点在1号和2号中点附近，且离2号近。但此时2号工作半径还是0，那么调用2号就不划算了，因为只要把1的工作半径增加一点就可以了。像这样，把1号定为A，把2号定为B：

   此时A的工作半径是4.5，B的工作半径是0，我们如果在这里放上一个C点，根据贪心，C是会投靠B的，那么B的工作半径白白增加了太多；如果我们让A来打这颗导弹，就只用扩大很小的范围了。

   得出结论：这种贪心是错的。

   那么我们换一种贪心？

   将点按与A的距离从小到大排序，检验每个点如果对A的工作半径影响小，就去A，否则去B。同时反过来对B也做一遍。

   30pnts？？？

   好吧看来这样也不行。

   根据上面所举的例子，我们重新梳理一下思路。如果一个拦截系统能照顾某个导弹，那么它一定能照顾所有比它近的导弹，这样就不用管比它近的了，那么这时候对没有被照顾的导弹，让他们都去投靠另一个拦截系统，那么另一个拦截系统的工作半径是这些剩下的导弹到该系统的最大距离。排序后，我们的状态就只剩下n种，那就是：离A系统前i近的被A照顾，剩下的被B照顾时所需的工作半径。在这些情况中取最小值就可以了。用前缀最大值来存储剩下的n-i个导弹到B系统的最大值，就可以用$ O(N)$枚举这些情况了。

    这种题可能还是见少了，总是往贪心方面想。但这种枚举做法也要会灵活运用。

Code：

#include<cstdio>
#include<algorithm>
int X[3],Y[3];
int x[120000],y[120000];
struct dis
{
    int dis1,dis2;//按到A的距离排序
    friend bool operator <(dis a,dis b)
    {
        return a.dis1<b.dis1;
    }
}d[120000];
int f[120000];
int main()
{
    scanf("%d%d%d%d",&X[1],&Y[1],&X[2],&Y[2]);
    int n,dis1,dis2;
    int mx1=0,mx2=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&x[i],&y[i]);
        d[i].dis1=(x[i]-X[1])*(x[i]-X[1])+(y[i]-Y[1])*(y[i]-Y[1]);
        d[i].dis2=(x[i]-X[2])*(x[i]-X[2])+(y[i]-Y[2])*(y[i]-Y[2]);
    }
    std::sort(d+1,d+1+n);
    for(int i=n;i>=1;i--)
    {
        if(d[i].dis2>f[i+1])
            f[i]=d[i].dis2;
        else
            f[i]=f[i+1];
    }
    int minn=123456789;
    for(int i=1;i<=n;i++)
        minn=std::min(minn,f[i+1]+d[i].dis1);
    printf("%d\n",minn);
    return 0;
}