洛谷 P2146 [NOI2015]软件包管理器 题解【树链剖分】【线段树】

点击量：218

   与其说是一道树剖题，不如说是学习了线段树的区间覆盖写法。

目录

题目描述

Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器，你可以通过一行命令安装某一个软件包，然后软件包管理器会帮助你从软件源下载软件包，同时自动解决所有的依赖（即下载安装这个软件包的安装所依赖的其它软件包），完成所有的配置。Debian/Ubuntu使用的apt-get，Fedora/CentOS使用的yum，以及OSX下可用的homebrew都是优秀的软件包管理器。

 

你决定设计你自己的软件包管理器。不可避免地，你要解决软件包之间的依赖问题。如果软件包A依赖软件包B，那么安装软件包A以前，必须先安装软件包B。同时，如果想要卸载软件包B，则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且，由于你之前的工作，除0号软件包以外，在你的管理器当中的软件包都会依赖一个且仅一个软件包，而0号软件包不依赖任何一个软件包。依赖关系不存在环（若有m(m≥2)个软件包A1,A2,A3,⋯,Am，其中A1依赖A2，A2依赖A3，A3依赖A4，……，A[m-1]依赖Am，而Am依赖A1，则称这m个软件包的依赖关系构成环），当然也不会有一个软件包依赖自己。

 

现在你要为你的软件包管理器写一个依赖解决程序。根据反馈，用户希望在安装和卸载某个软件包时，快速地知道这个操作实际上会改变多少个软件包的安装状态（即安装操作会安装多少个未安装的软件包，或卸载操作会卸载多少个已安装的软件包），你的任务就是实现这个部分。注意，安装一个已安装的软件包，或卸载一个未安装的软件包，都不会改变任何软件包的安装状态，即在此情况下，改变安装状态的软件包数为0。

 

输入输出格式

输入格式：
从文件manager.in中读入数据。

 

输入文件的第1行包含1个整数n，表示软件包的总数。软件包从0开始编号。

 

随后一行包含n−1个整数，相邻整数之间用单个空格隔开，分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。

 

接下来一行包含1个整数q，表示询问的总数。之后q行，每行1个询问。询问分为两种：

 

install x：表示安装软件包x

uninstall x：表示卸载软件包x

 

你需要维护每个软件包的安装状态，一开始所有的软件包都处于未安装状态。

 

对于每个操作，你需要输出这步操作会改变多少个软件包的安装状态，随后应用这个操作（即改变你维护的安装状态）。

 

输出格式：
输出到文件manager.out中。

 

输出文件包括q行。

 

输出文件的第i行输出1个整数，为第i步操作中改变安装状态的软件包数。

 

输入输出样例

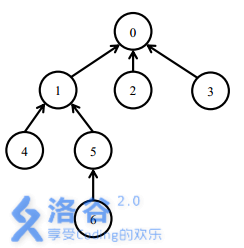
输入样例#1：

7

0 0 0 1 1 5 5

install 5

install 6

uninstall 1

install 4

uninstall 0

输出样例#1：

3

1

3

2

3

输入样例#2：

10

0 1 2 1 3 0 0 3 2

10

install 0

install 3

uninstall 2

install 7

install 5

install 9

uninstall 9

install 4

install 1

install 9

输出样例#2：

1

3

2

1

3

1

1

1

0

1

说明

【样例说明 1】

一开始所有的软件包都处于未安装状态。

 

安装5号软件包，需要安装0,1,5三个软件包。

 

之后安装6号软件包，只需要安装6号软件包。此时安装了0,1,5,6四个软件包。

 

卸载1号软件包需要卸载1,5,6三个软件包。此时只有0号软件包还处于安装状态。

 

之后安装4号软件包，需要安装1,4两个软件包。此时0,1,4处在安装状态。最后，卸载0号软件包会卸载所有的软件包。

 

【数据范围】

 

   比较裸的树链剖分，安装前统计0到要安装软件这条链上的数字和。安装时把这条链全部改为1，这一过程改变的数量为深度d[要安装软件]-之前统计的数字和。

   卸载前统计以当前软件为根的子树中数字和，改变的数量就是这个数，卸载时把这棵树上全部改成0。

   树剖的思路和板子在这篇文章写了。这里我记一下区间覆盖线段树的做法。

   线段树中把所有修改的+=改为=号是必须要有的，ask(query)基本不变，主要的区别在于change和lazytag+pushdown。change函数中因为做之前不知道要修改的差值，所以要在做之后求和左儿子右儿子。

   而lazytag+pushdown对于我之前的做法是有弊端的。我之前所写的lazy表示自己没有更新而携带lazytag，而我看网上OIer都写的是携带lazytag的点自己已更新，而pushdown自己的时候更新左右孩子的权值和lazytag，这样条理就清晰了很多。这个题（区间覆盖法）如果这样做的话会看得更清楚，而我原来的做法做这种题就会很麻烦，并且有可能出现多次冗余更新。以后我的线段树习惯应该就改过来了。

Code：

#include<cstdio>
#include<cstring>
#define ls (k<<1)
#define rs (k<<1|1)
#define mid (l+r>>1)
#define Mid (t[k].l+t[k].r>>1)
struct edge
{
    int n;
    int nxt;
    edge(int n,int nxt)
    {
        this->n=n;
        this->nxt=nxt;
    }
    edge()
    {
        nxt=-1;
    }
}e[201000];
int head[101000],ecnt=0;
void add(int from,int to)
{
    e[++ecnt]=edge(to,head[from]);
    head[from]=ecnt;
}

struct node
{
    int l,r,v,lazy;
    node(int l,int r,int v)
    {
        this->l=l;
        this->r=r;
        this->v=v;
        v=0;
        lazy=-1;
    }
    node(int l,int r)
    {
        this->l=l;
        this->r=r;
        v=0;
        lazy=-1;
    }
    node(){}

}t[400100];
void build(int k,int l,int r)
{
    t[k]=node(l,r,0);
    if(l==r)
        return;
    build(ls,l,mid);
    build(rs,mid+1,r);
}
void pushdown(int k)
{
    if(t[k].lazy==-1)
        return;
    t[k].v=(t[k].r-t[k].l+1)*t[k].lazy;//线段树为“改为”
    if(t[k].l==t[k].r)
    {
        t[k].lazy=-1;
        return;
    }
    t[ls].v=(t[ls].r-t[ls].l+1)*t[k].lazy;
    t[ls].lazy=t[k].lazy;
    t[rs].v=(t[rs].r-t[rs].l+1)*t[k].lazy;
    t[rs].lazy=t[k].lazy;
    t[k].lazy=-1;
}
int ask(int k,int l,int r)
{
    pushdown(k);
    if(l==t[k].l&&r==t[k].r)
        return t[k].v;
    if(r<=Mid)
        return ask(ls,l,r);
    else if(l>Mid)
        return ask(rs,l,r);
    return ask(ls,l,Mid)+ask(rs,Mid+1,r);
}
void change(int k,int l,int r,int x)
{
    if(t[k].l==l&&t[k].r==r)
    {
        t[k].v=(r-l+1)*x;
        t[k].lazy=x;
        //pushdown(k);
        return;
    }
    pushdown(k);
    if(r<=Mid)
        change(ls,l,r,x);
    else if(l>Mid)
        change(rs,l,r,x);
    else
    {
        change(ls,l,Mid,x);
        change(rs,Mid+1,r,x);
    }
    t[k].v=t[ls].v+t[rs].v;
    return;
}

//dfs求重链，
int d[100100],s[100100],sz[100100];
int fa[100100];
void dfs1(int x,int D)
{
    d[x]=D;
    sz[x]=1;
    s[x]=100001;
    for(int i=head[x];i!=-1;i=e[i].nxt)
    {
        if(!d[e[i].n])
        {
            fa[e[i].n]=x;
            dfs1(e[i].n,D+1);
            sz[x]+=sz[e[i].n];
            if(sz[e[i].n]>sz[s[x]])
                s[x]=e[i].n;
        }
    }
    return;
}
int dfn[100100],pnt[100100],cnt=0,over[100100];
int top[100100];
void dfs2(int x,int t)
{
    dfn[x]=++cnt;
    pnt[cnt]=x;
    top[x]=t;
    if(s[x]!=100001)
        dfs2(s[x],t);
    for(int i=head[x];i!=-1;i=e[i].nxt)
    {
        if(e[i].n==s[x])
            continue;
        dfs2(e[i].n,e[i].n);
    }
    over[x]=cnt;
    return;
}
int tree(int x)
{
    return ask(1,dfn[x],over[x]);
}
void treechange(int x)
{
    change(1,dfn[x],over[x],0);//改为0
}
int line(int x,int op)//op=2为修改
{
    int y=0,ans=0;
    int tx=top[x],ty=top[y];
    while(tx!=ty)
    {
        if(d[tx]<d[ty])//ty深一些
        {
            if(op==2)
                change(1,dfn[ty],dfn[y],1);
            else
                ans+=ask(1,dfn[ty],dfn[y]);
            y=fa[ty];
            ty=top[y];
        }
        else
        {
            if(op==2)
                change(1,dfn[tx],dfn[x],1);
            else
                ans+=ask(1,dfn[tx],dfn[x]);
            x=fa[tx];
            tx=top[x];
        }
    }
    if(dfn[x]<dfn[y])
    {
        if(op==2)
            change(1,dfn[x],dfn[y],1);
        else
            ans+=ask(1,dfn[x],dfn[y]);
    }
    else
    {
        if(op==2)
            change(1,dfn[y],dfn[x],1);
        else
            ans+=ask(1,dfn[y],dfn[x]);
    }
    return ans;
}

int main()
{
    memset(head,-1,sizeof(head));
    top[0]=0;
    fa[0]=0;
    int n,u;
    scanf("%d",&n);
    build(1,1,n);
    for(int i=1;i<n;i++)
    {
        scanf("%d",&u);
        add(u,i);
    }
    dfs1(0,1);
    dfs2(0,0);
    int m;
    scanf("%d",&m);
    char c[10];
    while(m--)
    {
        scanf("%s",c);
        if(c[0]=='i')
        {
            scanf("%d",&u);
            int k=line(u,1);
            line(u,2);
            printf("%d\n",d[u]-k);
        }
        else
        {
            scanf("%d",&u);
            int k=tree(u);
            treechange(u);
            printf("%d\n",k);
        }
    }
    return 0;
}